Ortobicupolă triunghiulară
În geometrie ortobicupola triunghiulară sau anticuboctaedrul este un poliedru convex construit prin unirea a două cupole triunghiulare (J3) prin bazele lor mari. Este prima din șirul infinit de bicupole. Este poliedrul Johnson J27. Având 14 de fețe, este un tetradecaedru.
| Ortobicupolă triunghiulară | |
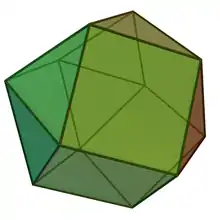 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J26 – J27 – J28 |
| Fețe | 14 (8 triunghiuri echilaterale, 6 pătrate)[1] |
| Laturi (muchii) | 24[1] |
| Vârfuri | 12[1] |
| χ | 2 |
| Configurația vârfului | 6 (32.42), 6 (3.4.3.4) |
| Grup de simetrie | D3h, [3,2], (*223), ordin 12 |
| Arie | ≈ 9,464 a2 (a = latura) |
| Volum | ≈ 2,357 a3 (a = latura) |
| Poliedru dual | Dodecaedru trapezorombic |
| Proprietăți | convexă |
| Desfășurată | |
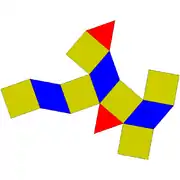 | |
Are un număr egal de pătrate și triunghiuri echilaterale la fiecare vârf, însă nu este tranzitivă pe vârfuri. Având o sferă mediană, este un poliedru canonic.
Relația cu cuboctaedrele
| Ortobicupolă triunghiulară | Girobicupolă triunghiulară |
|---|---|
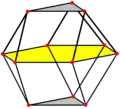 |
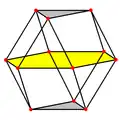 |
| Atât ortobicupola triunghiulară, cât și cuboctaedrul (girobicupola triunghiulară) conțin câte un hexagon central regulat. Ele pot fi divizate prin acest hexagon în perechi de cupole triunghiulare. | |
Ortobicupola triunghiulară are o oarecare asemănare cu cuboctaedrul, care ar fi similar cu girobicupola triunghiulară din nomenclatura poliedrelor Johnson — diferența este că cele două cupole triunghiulare care alcătuiesc ortobicupola triunghiulară sunt unite astfel încât perechi de fețe identice sunt adiacente (deci, „orto”); cuboctaedrul este îmbinat astfel încât triunghiurile sunt vecine cu pătratele și invers. Având în vedere o ortobicupolă triunghiulară, o rotație de 60° a unei cupole înainte de îmbinare dă un cuboctaedru. Prin urmare, un alt nume pentru ortobicupola triunghiulară este „anticuboctaedrul”.
Ortobicupola triunghiulară alungită (J35), care este construită prin alungirea ortobicupolei triunghiulare, are o relație specială (diferită) cu rombicuboctaedrul.
Dualul ortobicupolei triunghiulare este dodecaedrul trapezorombic, care are 6 fețe rombice și 6 trapezoidale și este similar cu dodecaedrul rombic.
Mărimi asociate
Următoarele formule pentru arie, A, volum, V, și raza sferei circumscrise, C sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Raza sferei circumscrise unei ortobicupole triunghiulare este același cu lungimea laturii (C = a).
Poliedre și faguri înrudiți
Fagurele cubic rectificat poate fi divizat și reconstruit ca o rețea de umplere a spațiului cu ortobicupole triunghiulare și piramide pătrate.[2]
Note
- Stephen Wolfram, "Triangular orthobicupola" from Wolfram Alpha. Retrieved July 23, 2010.
- en „J27 honeycomb”.