Prismă hexagonală metabiaugmentată
În geometrie prisma hexagonală metabiaugmentată este un poliedru convex construit prin augmentarea unei prisme hexagonale prin atașarea a două piramide pătrate (J1) pe două din fețele sale laterale care nu sunt adiacente sau opuse. Este poliedrul Johnson J56.[1][2] Când două astfel de piramide sunt atașate la fețele laterale opuse, rezultatul este o prismă hexagonală parabiaugmentată (J55). Poliedrul obținut prin atașarea piramidelor la fețele laterale adiacente nu este convex, prin urmare nu este un poliedru Johnson.
| Prismă hexagonală metabiaugmentată | |
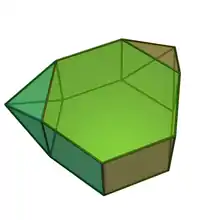 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J55 – J56 – J57 |
| Fețe | 14 (8 triunghiuri echilaterale 4 pătrate; 2 hexagoane)[1] |
| Laturi (muchii) | 26[1] |
| Vârfuri | 14[1] |
| χ | 2 |
| Configurația vârfului | 4 (42.6); 2 (34); 8 (32.4.6) |
| Grup de simetrie | C2v , [2], (*22), ordin 4 |
| Arie | ≈ 12,660 a2 (a = latura) |
| Volum | ≈ 3,069 a3 (a = latura) |
| Poliedru dual | – |
| Proprietăți | convexă |
| Desfășurată | |
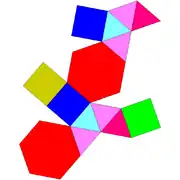 | |
Având 14 fețe, este un tetradecaedru.
Mărimi asociate
Pentru o prismă hexagonală augmentată cu lungimea laturilor egală cu 2 coordonatele vârfurilor sunt date de:
În acest caz, axa de simetrie a poliedrului va coincide cu axa Oz, iar două plane de simetrie vor coincide cu planele xOz și yOz.
Următoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Note
- en Stephen Wolfram, "Metabiaugmented hexagonal prism" from Wolfram Alpha. Retrieved January 4, 2023.
- en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603