Ortobicupolă pătrată

În geometrie ortobicupola pătrată este un poliedru convex construit prin unirea a două cupole pătrate (J₄) prin bazele lor octogonale astfel încât fețele adiacente ale celor două cupole sunt de același tip. Este a doua din șirul infinit de bicupole. Este poliedrul Johnson J₂₈. O rotire de 45° a uneia dintre cele două cupole înainte de unire produce girobicupola pătrată (J₂₉). Având 18 de fețe, este un octadecaedru. Nu este tranzitivă pe vârfuri.

Descriere
Ortobicupolă pătrată

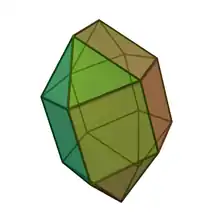(model 3D)
Tip	poliedru Johnson J₂₇ – J₂₈ – J₂₉
Fețe	18 (8 triunghiuri echilaterale, 10 pătrate)
Laturi (muchii)	32
Vârfuri	16
χ	2
Configurația vârfului	8 (3².4²), 8 (3.4³)
Grup de simetrie	D_4h, [4,2], (*224), ordin 16
Arie	≈ 13,464 a² (a = latura)
Volum	≈ 3,886 a³ (a = latura)
Proprietăți	convexă
Desfășurată

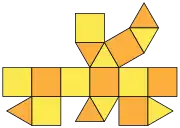Ortobicupola pătrată poate fi alungită prin inserarea unei prisme octogonale între cele două cupole ale sale pentru a produce un rombicuboctaedru, respectiv prin îndepărtarea unei prisme hexagonale neregulate se obține o bipiramidă pătrată alungită (J₁₅), care ea însăși este doar un tip de octaedru neregulat.

Poate fi construită dintr-un bisfenocingulum (J₉₀) prin înlocuirea benzii de triunghiuri de sus și de jos cu o bandă de dreptunghiuri, în timp ce se păstrază două sfenocoroane (J₈₆) opuse.

Mărimi asociate

Coordonatele celor opt vârfuri de pe ecuator pentru latura a o unitate sunt:[1][2]

\left(\pm {\frac {1}{2}}(1+{\sqrt {2}}),\pm {\frac {1}{2}},0\right),\left(\pm {\frac {1}{2}},\pm {\frac {1}{2}}(1+{\sqrt {2}}),0\right),

iar a celorlalte opt vârfuri sunt:[1]

\left(\pm {\frac {1}{\sqrt {2}}},0,\pm {\frac {1}{\sqrt {2}}}\right),\left(0,\pm {\frac {1}{\sqrt {2}}},\pm {\frac {1}{\sqrt {2}}}\right).

Formulele pentru arie $A$ și volum $V$ sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]

A=2(5+{\sqrt {3}})\,a^{2}\approx 13,464101\,a^{2}

V=2\left(1+{\frac {2{\sqrt {2}}}{3}}\right)a^{3}\approx 3,885618\,a^{3}

Ortobicupola pătrată formează faguri în care spațiul este umplut și cu tetraedre; cu cuburi și cuboctaedre; cu tetraedre și cuburi; cu piramide pătrate, tetraedre și diverse combinații de cuburi, piramide pătrate alungite și/sau bipiramide pătrate alungite.[3]

en Wolfram Research, Inc. (2020). „Wolfram|Alpha Knowledgebase”. Champaign, IL. PolyhedronData[{"Johnson", 4}]
es Sapiña, R. „Area and volume of the Johnson solid J₄”. Problemas y Ecuaciones. ISSN 2659-9899. Accesat în 16 iulie 2020.
en „J28 honeycomb”.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.