Cupolă triunghiulară

În geometrie cupola triunghiulară este o cupolă la care fața opusă bazei este un triunghi echilateral, iar baza este un hexagon. Este poliedrul Johnson J₃. Poate fi văzută ca o jumătate dintr-un cuboctaedru. Având 8 fețe, este un octaedru neregulat.

Descriere
Cupolă triunghiulară

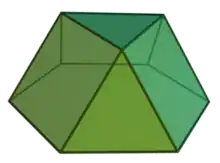(model 3D)
Tip	poliedru Johnson J₂ – J₃ – J₄
Fețe	8 (4 triunghiuri echilaterale, 3 pătrate, 1 hexagon regulat)
Laturi (muchii)	15
Vârfuri	9
χ	2
Configurația vârfului	6 (3.4.6); 3 (3.4.3.4)
Grup de simetrie	C_3v, [3], (*33), ordin 6
Arie	≈ 7,330 a² (a = latura)
Volum	≈ 1,179 a³ (a = latura)
Poliedru dual	C1000dJ3[1]
Proprietăți	convexă
Desfășurată

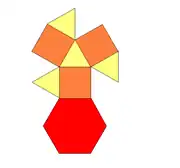Mărimi asociate

Următoarele formule pentru înălțime $h$ , arie $A$ și volum $V$ sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[2][3]

h={\frac {\sqrt {6}}{3}}a\approx 0,816496\,a

A=\left(3+{\frac {5{\sqrt {3}}}{2}}\right)a^{2}\approx 7,330127\,a^{2}

V={\frac {5{\sqrt {2}}}{6}}\,a^{3}\approx 1,178511\,a^{3}

Poliedre și faguri înrudiți

Poliedru dual

Dualul cupolei triunghiulare are 6 fețe triunghiulare și 3 fețe romboidale:[1]

Dualul cupolei triunghiulare	Desfășurata dualului

Alte cupole convexe

Familia cupolelor cu fețe regulate există până la n = 5 (pentagon) și chiar mai mult dacă la cupole se folosesc triunghiuri isoscele.

Familia cupolelor convexe
n	2	3	4	5	6
Schläfli	{2} \|\| t{2}	{3} \|\| t{3}	{4} \|\| t{4}	{5} \|\| t{5}	{6} \|\| t{6}
Cupolă	Cupolă digonală	Cupolă triunghiulară	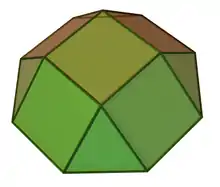Cupolă pătrată	Cupolă pentagonală	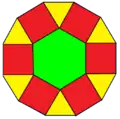Cupolă hexagonală (plată)
Poliedre uniforme înrudite	Prismă triunghiulară	Cubocta- edru	Rombi- cubocta- edru	Romb- icosidodeca- edru	Pavare rombi- trihexagonală

Alte poliedre

Cupolă triunghiulară augmentată

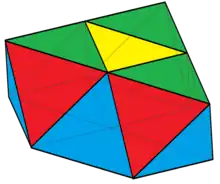
Cupola triunghiulară poate fi augmentată cu 3 piramide pătrate, lăsând fețele adiacente coplanare. Acesta nu este un poliedru Johnson din cauza fețelor sale coplanare. Contopind aceste triunghiuri coplanare în triunghiuri mai mari, topologic aceasta este o altă cupolă triunghiulară cu fețele laterale trapeze isoscele. Dacă se păstrează toate triunghiurile și se înlocuiește hexagonul de la bază cu 6 triunghiuri, se generează un deltaedru coplanar cu 22 de fețe.

Faguri

Cupola triunghiulară poate tesela spațiul împreună cu piramida pătrată și/sau octaedrul,[4] la fel cum octaedrele și cuboctaedrele pot umple spațiul.

Note

en C1000dJ3, polyHedronisme v.0.2.1, accesat 2022-06-11
en Stephen Wolfram, "Triangular cupola" from Wolfram Alpha. Retrieved July 20, 2010
es Sapiña, R. „Area and volume of the Johnson solid J₃”. Problemas y Ecuaciones. ISSN 2659-9899. Accesat în 8 septembrie 2020.
en „J3 honeycomb”.

Legături externe

en Eric W. Weisstein, Triangular cupola la MathWorld.
en Eric W. Weisstein, Johnson solid la MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[pH-1] C1000dJ3, polyHedronisme v.0.2.1, accesat 2022-06-11

[2] Stephen Wolfram, "Triangular cupola" from Wolfram Alpha. Retrieved July 20, 2010

[pye-3] s Sapiña, R. „Area and volume of the Johnson solid J₃”. Problemas y Ecuaciones. ISSN 2659-9899. Accesat în 8 septembrie 2020.

[4] „J3 honeycomb”.