Tetraedru triakis

În geometrie, un tetraedru triakis este un poliedru Catalan cu 12 fețe. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Dualul tetraedrului triakis este tetraedrul trunchiat.

Descriere
Tetraedru triakis

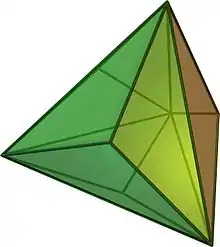(animație și model 3D)
Tip	Poliedru Catalan
Fețe	12 (triunghiuri isoscele)
Laturi (muchii)	18
Vârfuri	8
χ	2
Configurația feței	V3.6.6
Simbol Conway	kT
Diagramă Coxeter
Grup de simetrie	T_d, A₃, [3,3], (*332), ordin 24
Grup de rotație	T, [3,3]⁺, (332), ordin 12
Arie	≈ 5,528 a² (a = latura mică)
Volum	≈ 0,982 a³ (a = latura mică)
Unghi diedru	129° 31′ 16″ = arccos(−7/11)
Poliedru dual	Tetraedru trunchiat
Proprietăți	Poliedru convex, tranzitiv pe fețe
Desfășurată

Dual: Tetraedru trunchiat

Tetraedrul triakis poate fi considerat un tetraedru cu o piramidă triunghiulară adăugată pe fiecare față, adică este un Kleetop al tetraedrului. Este foarte asemănător cu desfășurata unui 5-celule, deoarece dacă desfășurata unui tetraedru este un triunghi cu alte triunghiuri adăugate la fiecare latură, desfășurata a 5-celule este un tetraedru cu piramide atașate la fiecare față. Această interpretare este exprimată prin nume.

Lungimea laturilor mai scurte este de 3/5 din cea a laturilor mai lungi.[1] Dacă tetraedrul triakis are lungimea laturii mai scurte 1, are aria 5/3√11 și volumul 25/36√2.

Coordonate carteziene

Coordonatele carteziene ale celor 8 vârfuri ale unui tetraedru triakis centrat în origine sunt punctele (±5/3, ±5/3, ±5/3) cu un număr par de semne minus, împreună cu punctele (±1, ±1, ±1) cu un număr impar de semne minus:

(5/3, 5/3, 5/3), (5/3, −5/3, −5/3), (−5/3, 5/3, −5/3), (−5/3, −5/3, 5/3)
(−1, 1, 1), (1, −1, 1), (1, 1, −1), (−1, −1, −1)

Lungimea laturilor mai scurte ale acestui tetraedru triakis este egală cu $2{\sqrt {2}}$ . Fețele sunt triunghiuri isoscele cu un unghi obtuz și două unghiuri ascuțite. Unghiul obtuz are valoarea $\arccos(-7/18)\approx 112,885\,380\,476\,16^{\circ }$ iar cele ascuțite $\arccos(5/6)\approx 33,557\,309\,761\,92^{\circ }$ .

Simetrie tetartoidă

Tetraedrul triakis poate fi construit ca o limită degenerată a unui tetartoid:

Exemple de variații tetartoide
Tetartoid 0% (Dodecaedru regulat)	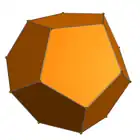Tetartoid 10%	Tetartoid 20%	Tetartoid 30%
Tetartoid 60%	Tetartoid 80%	Tetartoid 95%	Tetartoid 100% (Tetraedru triakis)

Proiecții ortogonale

Proiecții ortogonale (grafuri)
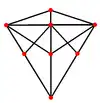
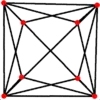
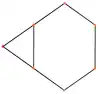
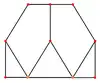
Centrat pe	Latura scurtă	Față	Vîrf	Latura lungă
Tetraedru triakis
(Dual) Tetraedru trunchiat
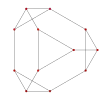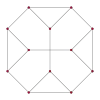Simetrie proiectivă	[1]		[3]	[4]

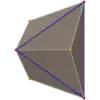
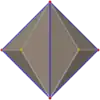
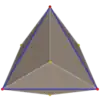
Proiecții ortogonale (corpuri)
Tetraedru triakis
Compus dual
(Dual) Tetraedru trunchiat
Simetrie proiectivă	[1]	[2]	[3]

Variații

5-celule

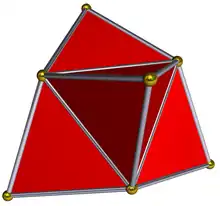
Un tetraedru triakis cu fețe triunghiulare echilaterale este desfășurata politopului regulat cvadridimensional cunoscut sub numele de 5-celule.

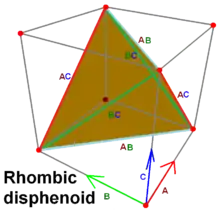
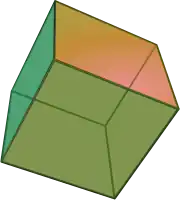
Dacă triunghiurile sunt dreptunghice isoscele, fețele vor fi coplanare și vor forma un volum cubic. Acest lucru poate fi văzut prin adăugarea celor 6 laturi ale tetraedrului în interiorul unui cub (bisfenoid rombic).

Stelări

Această figură chirală este una dintre cele treisprezece stelări permise de regulile lui Miller.[2]

Poliedre înrudite

Tetraedru triakis sferic

Tetraedrul triakis este o parte a unei secvențe de poliedre și pavări, extinzându-se în planul hiperbolic. Aceste figuri tranzitive pe fețe au simetrie de reflexie (*n32) în Notația orbifold.

Variante ale pavărilor trunchiate cu simetrie *n32: t{n,3}
Smetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.	Hiperbolice necompacte
Smetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figuri trunchiate
Schläfli	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Figuri triakis
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Familia poliedrelor tetraedrice uniforme
Simetrie: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duale ale poliedrelor uniforme

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Note

en „Triakis Tetrahedron - Geometry Calculator”.
en H.S.M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-Nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26

Bibliografie

en Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
en Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 14, Triakistetrahedron)
en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008). The Symmetries of Things, ISBN: 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis tetrahedron )

Legături externe

en Eric W. Weisstein, Triakis tetrahedron la MathWorld.
en Eric W. Weisstein, Catalan solid la MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] „Triakis Tetrahedron - Geometry Calculator”.

[2] H.S.M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-Nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26