Bitrunchi

În geometrie un bitrunchi n-gonal[1] este un poliedru ale cărui vârfuri sa află situate toate în trei plane paralele. În cele trei plane vârfurile formează trei n-goane, cel din planul din mijloc fiind cel mai mare și de obicei cele de sus și de jos sunt congruente.

Descriere
Bitrunchi

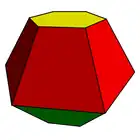Exemplu: bitrunchi hexagonal
Fețe	2 n-goane, 2n trapeze
Laturi (muchii)	5n
Vârfuri	3n
χ	2
Grup de simetrie	D_nh, [n,2], (*n22)
Grup de rotație	D_n, [n,2]⁺, (n22)
Poliedru dual	bipiramidă alungită
Proprietăți	convex

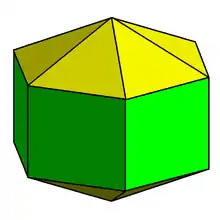
Dualul exemplului de mai sus, bipiramida hexagonală alungită

Poate fi construit din două trunchiuri congruente unite pe un plan de simetrie și, de asemenea, ca o bipiramidă cu cele două vârfuri polare trunchiate.

Poliedrele lor duale sunt bipiramidele alungite.

Formule

Pentru un bitrunchi regulat, cu laturile $n$ -poligonului ecuatorial $a$ , laturile $n$ -poligoanelor bazelor $b$ și semiînălțimea (jumătate din distanța dintre planele celor două baze) $h$ formulele de calcul ale ariei laterale $A l$ , ariei totale $A$ și a volumului $V$ sunt:[2]

A_{l}=n(a+b){\sqrt {\left({\frac {a-b}{2}}\cot {\frac {\pi }{n}}\right)^{2}+h^{2}}}\,,

A=A_{l}+n{\frac {b^{2}}{2\tan {\frac {\pi }{n}}}}\,,

V=n{\frac {a^{2}-b^{2}}{6\tan {\frac {\pi }{n}}}}h\,.

Exemple

Există un număr infinit de bitrunchiuri, trei dintre ele fiind dualele a trei poliedre Johnson, J₁₄–J₁₆. În general, un bitrunchi n-gonal are fețele 2n trapeze și 2 n-goane și este dualul bipiramidelor alungite.

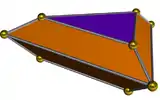
Bitrunchi triunghiular	Bitrunchi pătrat	Bitrunchi pentagonal	Bitrunchi hexagonal

6 trapeze, 2 triunghiuri. Dualul bipiramidei triunghiulare alungite, J₁₄	8 trapeze, 2 pătrate. Dualul bipiramidei pătrate alungite, J₁₅	10 trapeze, 2 pentagoane. Dualul bipiramidei pentagonale alungite, J₁₆	12 trapeze, 2 hexagoane. Dualul bipiramidei hexagonale alungite

Note

D. Berciu, O colecție de antichități din județul Romanați: Gh. Georgescu-Corabia Arhivat în 12 noiembrie 2022, la Wayback Machine., Buletinul Comisiunii Monumentelor Istorice, anul XXVII, 1934, pp. 74–84, accesat 2022-06-10
de Regelmäßiges Bifrustum - Rechner, rechneronline.de, accesat 2022-06-28

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] D. Berciu, O colecție de antichități din județul Romanați: Gh. Georgescu-Corabia Arhivat în 12 noiembrie 2022, la Wayback Machine., Buletinul Comisiunii Monumentelor Istorice, anul XXVII, 1934, pp. 74–84, accesat 2022-06-10

[rechner-2] Regelmäßiges Bifrustum - Rechner, rechneronline.de, accesat 2022-06-28