Glosar de numere întregi
Prezentul glosar de numere întregi conține termeni din domeniul claselor de numere întregi și a altor domenii fundamentale ale matematicii ca: aritmetică sau teoria numerelor. Pentru celelalte domenii ale matematicii, ca algebra, analiza matematică și geometria, vedeți celelalte glosare din categoria: Glosare de matematică.
A
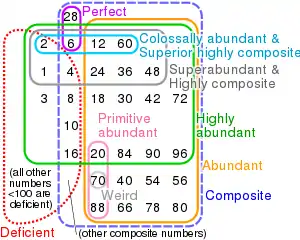
Diagrama Euler a numerelor abundente, abundente primitive, extrem abundente, superabundente, colosal abundente, extrem compuse, extrem compuse superioare, ciudate și perfecte mai mici decât 100 în raport cu numerele deficiente și compuse.
- abundent sau excesiv, un număr care este mai mic decât suma alicotă a divizorilor săi.
- Ahile, un număr puternic care nu este pătrat perfect.
- amiabil. O pereche de numere amiabile este formată din două numere între care există următoarea relație: suma alicotă a divizorilor fiecăruia dintre ele este egală cu celălalt număr.
- Apéry, un număr An exprimat cu ajutorul coeficienților binomiali ca suma de la k = 0 la k = n a produselor C(n, k)2 * C(n + k, k)2. Sau
- aproape perfect, un număr natural n care are proprietatea că 2*n – 1 = σ(n)
- Armstrong sau narcisist, un număr n, cu un număr de k cifre, care este egal cu suma cifrelor sale ridicate la puterea k.[2]
- aspirant, numărul natural cu proprietatea că seria sa alicotă se termină într-un număr perfect.[3] 25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685
- automorf, un număr al cărui pătrat într-o bază dată „se termină” cu aceleași cifre ce compun numărul însuși.[4] 0, 1, 5, 6, 25, 76, 376, 625, 9376, 90625, 109376, 890625, 2890625, 7109376, 12890625, 87109376
B
C
- Carmichael
- Carol
- Catalan
- Catalan-Mersenn
- centrat poligonal, o clasă de serii de numere figurative, fiecare formată dintr-un punct central, înconjurat de straturi poligonale cu un număr constant de laturi:
- centrat triunghiular
- centrat pătratic
- centrat pentagonal
- centrat hexagonal
- centrat heptagonal
- centrat octogonal
- centrat nonagonal
- centrat decagonal
- centrat endecagonal
- centrat dodecagonal
- centrat tetraedric - număr figurativ centrat care dă numărul de puncte dintr-un model tridimensional format dintr-un punct înconjurat de straturi tetraedrice concentrice de puncte; altă denumire: centrat tetraedral.
- centrat cubic - număr figurativ centrat care dă numărul de puncte dintr-un model tridimensional format dintr-un punct înconjurat de straturi cubice concentrice de puncte, cu puncte pe fețele pătrate ale stratului i.
- centrat octaedric sau centrat octaedral
- centrat dodecaedric sau centrat dodecaedral
- centrat icosaedric sau centrat icosaedral
- Chernick
- ciclic
- ciudat
- colosal abundent
- columbian
- compozitorial
- compus, un număr care are cel puțin un divizor pozitiv în afară de 1 și el însuși
- concatenat
- Connell
- congruent
- consecutiv
- consecutiv Smarandache
- Conway-Guy
- coprime sau prime între ele, numere care nu au alt divizor comun în afară de 1, sau, altfel spus, dacă cel mai mare divizor comun al lor este 1.
- coprimorial
- cototativ
- cubic, este rezultatul ridicării sale la puterea a treia: cu alte cuvinte numărul înmulțit cu el însuși de trei ori.
- Cullen
- Cunningham
E
- echidigital
- egiptean
- EPRN
- Erdős-Woods
- Euclid
- Euclid-Mullin
- excesiv
- exponențial perfect
- extravagant
- extrem abundent
- extrem compus
- extrem compus superior
- extrem cototient
- extrem totient
F
- factorial
- fericit
- Fermat
- Fibonacci
- fibonorial
- figurativ
- Fortunate
- Franel
- Friedman
- frugal
- Fürer, algoritm ~ - algoritm de înmulțire a numerelor întregi pentru numere întregi extrem de mari, cu complexitate foarte mică.
K
M
- maleabil
- Markov
- Matijasevič
- Mersenn
- Mian-Chowla
- minunat
- Moser-de Bruijn
- Motzkin
- multifactorial
- multiperfect
N
- Narayana
- narcisist
- natural
- nefericit
- neobișnuit
- neuniform
- Niven
- nontotient
- norocos Euler
- norocos Ulam
- Newman-Shanks-Williams
P
- Padovan
- palindromic, un număr care citit de la stânga la dreapta sau de la dreapta la stânga rămâne neschimbat
- pandigital
- par - un număr care are forma n = 2p , unde p este un număr întreg.
- de partiții - numărul de moduri în care poate fi partiționat un număr întreg.
- pătratic - un număr care este pătratul unui alt număr
- Pell - șir de numere egale cu numitorii care aproximează din ce în ce mai fidel rădăcina pătrată a lui 2
- Pell-Lucas
- perfect
- perfect totient
- perfect unitar
- Perrin
- persistent
- Pisano
- pitagoreic
- platonician
- poligonal
- politicos
- potrivit
- Poulet
- practic
- prietenos
- prietenos Smarandache
- prim
- prim absolut
- prim aditiv
- prim aproximativ fibonorial
- prim asigurat
- prim bun
- prim Chen
- prim circular
- prim constelație
- prim echilibrat
- prim elitist
- prim Euler
- prim factorial
- prim Fibonacci-Wieferich
- prime gemene
- prim interior
- prim izolat
- prim înlănțuite Cunningham
- prim înlănțuit geamăn
- prim Labos
- prim lung
- prim mănunchi
- prim Mersenne
- prim Mills
- prim minimal
- prim permutabil
- prim Pierpont
- prim Pillai
- prim plat
- prim probabil
- prim progresiv
- prim quasi-fibonorial
- prim Ramanujan
- prim reversibil
- prim Rowland
- prim sexy
- prim slab
- prim Smarandache
- prim Solinas
- prim Sophie Germain
- prim Stern
- prim subțire
- prim tare
- prim titanic
- prim trunchiabil
- prim unic
- prim verișor
- prim Wagstaff
- prim Wall-Sun-Sun
- prim Wieferich
- primitiv
- primorial
- Proth
- pseudoperfect
- pseudoprim
- pseudoprim Catalan
- pseudoprim Cipolla
- pseudoprim Euler
- pseudoprim Fermat
- pseudoprim Fibonacci
- pseudoprim Lucas
- pseudoprim Perrin
- pseudoprim tare
- pseudo-Smarandache
- puternic, un număr pozitiv m cu proprietatea că, dacă este divizibil cu numărul prim p, atunci este divizibil și cu p2
Q
- quasi-amiabil
- quasi-Carmichael
- quasi-perfect
S
- Sarrus
- Schröder
- Segner
- semiperfect
- semiprim
- sfenic
- Sierpiński
- slab totient
- Smarandache
- Smarandache-Fibonacci
- Smarandache-Radu
- Smarandache-Wellin
- Smith
- sociabil
- solitar
- Somos
- Stern-Brocot
- Størmer
- subfactorial
- sublim
- superabundent
- superfactorial
- superperfect
- superprimorial
- super-Poulet
- sumă alicotă, suma divizorilor alicoți.
T
- tablou triunghiular - șir dublu indexat în care lungimea fiecare rând este egală cu indicele rândului.
- tetraedric
- Thabit
- tort
- totativ
- triunghiular
- triunghiul armonic al lui Leibnitz - tablou triunghiular cu fracții unitare.
- triunghiul lui Bell - tablou triunghiular analog cu triunghiul lui Pascal.
- triunghiul lui Bernoulli - tablou triunghiular cu sume parțiale de coeficienți binomiali.
- triunghiul lui Catalan - tablou triunghiular cu diferențe de coeficienți binomiali.
- triunghiul lui Floyd - tablou triunghiular cu numerele naturale, folosit în informatică drept exercițiu.
- triunghiul lui Hosoya - tablou triunghiular cu numere Fibonacci.
- triunghiul lui Lozanić - tablou triunghiular folosit în chimie.
- triunghiul lui Pascal - tablou triunghiular cu coeficienții binomiali.
- triunghiul numerelor de partiții - tablou triunghiular cu numărul de partiții al numerelor întregi.
- triunghiul trinomial - tablou triunghiular cu coeficienții trinomiali.
Note
- Șirul A005259 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- Șirul A005188 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- Șirul A063769 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- Șirul A003226 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
Bibliografie
- Marius Coman, Enciclopedia matematică a claselor de numere întregi
- Caius Iacob, Dicționar de matematici generale, Editura Enciclopedică Română, 1974
- Romulus Cristescu, Dicționar de analiză matematică, Editura Științifică și Enciclopedică, 1989
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.