Triunghiul lui Bernoulli

În matematică triunghiul lui Bernoulli este un tablou triunghiular ale cărui elemente sunt sumele parțiale ale coeficienților binomiali. Pentru orice întreg nenegativ n și pentru orice întreg k între 0 și n, componenta din rândul n și coloana k este dată de:

${\displaystyle \sum _{p=0}^{k}{n \choose p},}$

Deoarece numerele compozițiilor lui n+1 în k+1 partiții ordonate formează triunghiul lui Pascal, numerele de compoziții ale lui n+1 în k+1 sau mai puține partiții ordonate formează triunghiul lui Bernoulli

Derivarea triunghiului lui Bernoulli (text gras albastru) din triunghiul lui Pascal (italice roz)

adică suma primilor k coeficienți binomiali de ordinul n.[1] Primele rânduri ale triunghiului lui Bernoulli sunt:

${\displaystyle {\begin{array}{cc|cccccc}&k&0&1&2&3&4&5\\n&&\\\hline 0&&1\\1&&1&2\\2&&1&3&4\\3&&1&4&7&8\\4&&1&5&11&15&16\\5&&1&6&16&26&31&32\end{array}}}$

Similar cu triunghiul lui Pascal, fiecare componentă a triunghiului lui Bernoulli este suma a două componente din rândul precedent, cu excepția ultimului număr din fiecare rând, care este dublul ultimului număr din rândul precedent. De exemplu, dacă se notează ${\displaystyle B_{n,k}}$ componenta din rândul n și coloana k, atunci:

${\displaystyle {\begin{aligned}B_{n,k}=&B_{n-1,k}+B_{n-1,k-1}&{\mbox{ dacă }}&k<n\\B_{n,k}=&2B_{n-1,k-1}&{\mbox{ dacă }}&k=n\end{aligned}}}$

Șiruri din On-Line Encyclopedia of Integer Sequences în triunghiul lui Bernoulli

Ca și în triunghiul lui Pascal și în alte triunghiuri construite similar,[2] sumele componentelor de-a lungul diagonalelor din triunghiul lui Bernoulli sunt numere Fibonacci.[3]

Deoarece a treia coloană a triunghiului lui Bernoulli (k = 2) este un număr triunghiular plus unu, el formează șirul tăietorului leneș pentru n tăieturi, unde n ≥ 2.[4] A patra coloană (k = 3) este analogul tridimensional, cunoscut ca numere de tort, pentru n tăieturi, unde n ≥ 3.[5]

A cincea coloană (k = 4) dă numărul maxim de regiuni în problema divizării unui disc în regiuni pentru n+1 puncte, unde n ≥ 4.[6]

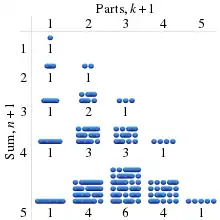
În general, a (k+1)-a coloană dă numărul maxim de regiuni din spațiul k-dimensional format din n−1 hiperplane (k−1)-dimensionale, pentru n ≥ k.[7] De asemenea, dă numărul de compoziții (partiții ordonate) ale lui n+1 în k+1 sau mai puține părți.[8]