Pavare triunghiulară de ordin infinit
În geometrie pavarea triunghiulară de ordin infinit este o pavare regulată a planului hiperbolic. Este reprezentată de simbolul Schläfli {3,∞}. Toate vârfurile sunt ideale, situate la „infinit” și văzute la limita proiecției pe discul hiperbolic Poincaré.
| Pavare triunghiulară de ordin infinit | |
 | |
| Pe modelul discului Poincaré al planului hiperbolic | |
| Descriere | |
|---|---|
| Tip | pavare uniformă hiperbolică |
| Configurația vârfului | 3∞ |
| Simbol Wythoff | ∞ | 3 2 |
| Simbol Schläfli | {3,∞} |
| Diagramă Coxeter |        |
| Grup de simetrie | [∞,3], (*∞32) |
| Grup de rotație | [∞,3]+, (∞32) |
| Poliedru dual | pavare apeirogonală de ordinul 3 |
| Proprietăți | tranzitivă pe vârfuri, laturi și fețe |
Simetrie
O formă cu simetrie inferioară are culori alternate și este reprezentată prin simbolul ciclic {(3,∞,3)}, 
. Pavarea reprezintă, de asemenea, domeniile fundamentale ale simetriei *∞∞∞, care poate fi văzută cu 3 culori de linii reprezentând 3 plane de oglindire ale construcției.
 Pavare colorată alternat |
 Simetrie *∞∞∞ |
 Circumscriere apoloniană cu simetrie *∞∞∞ |
Poliedre și pavări înrudite
Pavarea duală
{3,3,∞} are figura vârfului {3,∞}
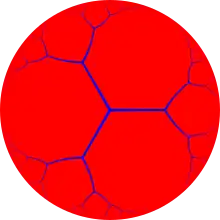
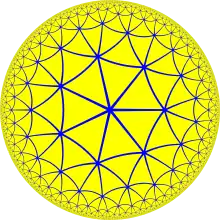
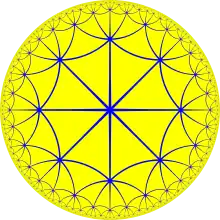
Această pavare este înrudită topologic cu șirul poliedrelor regulate cu simbolul Schläfli {3,p}.
| Variante de pavări regulate cu simetrie: *n32 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sferice | Euclid. | Hiperb. compacte | Paraco. | Hiperbolice necompacte | |||||||
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
| Pavări uniforme paracompacte din familia [∞,3] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
|
|
|
|
|
|
|
 |
 |
|
|
 =  |
= |
= |
|
= or  |
= or |
=  | ||||
|
 |
 |
 |
|
 |
 |
 |
 |
 | |
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| Duale uniforme | ||||||||||
 |
|
|
|
|
|
|
 |
|
| |
|
 |
 |
 |
|
 |
 |
 |
 |
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
| Pavări uniforme hiperbolice paracompacte din familia [(∞,3,3)]. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie: [(∞,3,3)], (*∞33) | [(∞,3,3)]+, (∞33) | ||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
|
 |
 |
 |
 |
 |
 |
| ||||
| (∞,∞,3) | t0,1(∞,3,3) | t1(∞,3,3) | t1,2(∞,3,3) | t2(∞,3,3) | t0,2(∞,3,3) | t0,1,2(∞,3,3) | s(∞,3,3) | ||||
| Pavări duale | |||||||||||
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||||
|
|
||||||||||
| V(3.∞)3 | V3.∞.3.∞ | V(3.∞)3 | V3.6.∞.6 | V(3.3)∞ | V3.6.∞.6 | V6.6.∞ | V3.3.3.3.3.∞ | ||||
Alte pavări triunghiulare de ordin infinit
O pavare triunghiulară neregulată de ordin infinit poate fi generată printr-un proces recursiv dintr-un triunghi central, așa cum se arată în figura alăturată.
Bibliografie
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- en H.S.M. Coxeter (). „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. ISBN 0-486-40919-8. LCCN 99035678.
Vezi și
Legături externe
Materiale media legate de pavare triunghiulară de ordin infinit la Wikimedia Commons- en Eric W. Weisstein, Hyperbolic tiling la MathWorld.
- en Eric W. Weisstein, Poincaré hyperbolic disk la MathWorld.
- en Hyperbolic and Spherical Tiling Gallery Arhivat în , la Wayback Machine.
| Periodice |
|   | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Aperiodice | |||||||||
| Altele |
| ||||||||
| După tipul vârfurilor |
| ||||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.