Pavare apeirogonală de ordinul 6

În geometrie pavarea apeirogonală de ordinul 6 este o pavare regulată a planului hiperbolic. Este reprezentată de simbolul Schläfli {∞,6}, având șase apeirogoane în jurul fiecărui vârf. Fiecare apeirogon este înscris într-un oriciclu.

Pavare apeirogonala
de ordinul 6
Pe modelul discului Poincaré al planului hiperbolic
Descriere
Tippavare uniformă hiperbolică
Configurația vârfului∞6
Simbol Wythoff6 | ∞ 2
Simbol Schläfli{∞,6}
Diagramă Coxeter
Grup de simetrie[∞,6], (*∞62)
Grup de rotație[∞,6]+
Poliedru dualpavare hexagonală de ordin infinit
Proprietățitranzitivă pe vârfuri, laturi și fețe

Simetrie

Pavarea din imaginea din stânga reprezintă liniile de oglindire ale simetriei *6∞. Duala acestei pavări reprezintă domeniile fundamentale ale simetriei [∞,5*] cu notația orbifold *∞∞∞∞∞∞, un domeniu hexagonal cu șase vârfuri ideale.

Pavarea apeirogonală de ordinul 6 poate fi colorată uniform cu 6 apeirogoane colorate în jurul fiecărui vârf și diagrama Coxeter:

Poliedre și pavări înrudite

Această pavare este legată topologic ca parte a secvenței de poliedre regulate și pavări cu șase fețe pe vârf, pornind de la pavarea triunghiulară, cu simbolul Schläfli {n,6} și diagrama Coxeter , cu n mergând până la infinit.

Pavări regulate cu simetria {n,6}
Sferică Euclidiană Hiperbolice

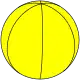{2,6}
{3,6}
{4,6}
{5,6}
{6,6}
{7,6}
{8,6}
 ...
{∞,6}

Bibliografie
  • en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • en „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. . ISBN 0-486-40919-8. LCCN 99035678.

Vezi și

Legături externe
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.