Probability threshold in ROC curve analyses

Question

When conducting a logistic regression analysis in SPSS, a default threshold of 0.5 is used for the classification table. Consequently, individuals with a predicted probability < 0.5 are assigned to Group "0", while those with a predicted probability > 0.5 are assigned to Group "1". However, this threshold may not be the one that maximizes sensitivity and specificity. In other words, adjusting the threshold could potentially increase the overall accuracy of the model.

To explore this, I generated a ROC curve, which provides both the curve itself and the coordinates. I can choose a specific point on this curve.

My question now is, how do I translate from this ROC curve or its coordinates to the probability that I need to specify as the classification cutoff in SPSS (default: 0.50)? The value must naturally fall between 0 and 1.

1. Do I simply need to select an X-value from the coordinate table where I have the best sensitivity/specificity (top left corner) and plug it into the formula for P(Y=1)?

2. What do I do when I have more than one predictor (X) variable? Choose the best point/coordinate for both predictors separately and plug in the values into the equation for P(Y=1) and calculate the new cutoff value?

Answer 1

Logistic regression is not strictly a classification method. It produces a linear predictor, a function of all the predictor values, that estimates the log-odds of a binary outcome, which then can be translated into outcome probability.

The path along the ROC curve is equivalent to a path along the values of that linear predictor (or its associated predicted probabilities). Using a high predicted probability as a cutoff, you get a low fraction of true positives and a low fraction of false positives (bottom left of the curve). Using a low predicted probability as a cutoff, you get high proportions of both true and false positives (top right of the curve). The R ROCR package has a nice way of visualizing the predicted probabilities along the ROC curve, as illustrated in a vignette and in this online text. There might be a similar display available in SPSS, but I don't use that software.

So to answer your second question, for a multiple logistic regression you use the desired value of the linear predictor (or predicted probability), based on all the predictors together, that puts you where you want along the ROC curve.

To answer your first question, do not fall into the trap of always using p = 0.5 (the usual hidden software default) or the "top left" of the ROC curve ("best sensitivity/specificity") as the probability cutoff. The proper choice of cutoff (if one is really necessary) should take into account the relative costs of false-negative and false-positive classifications. See for example this page and its links, particularly those from this answer. Briefly, the optimal probability cutoff is determined by the ratio of misclassification costs. That's part of the application of the logistic regression model, not of the model itself.

Added in response to comments

In general with regression, and particularly with binary (e.g., logistic) regression, it's a mistake to do separate models for each predictor. Even in ordinary linear regression, a model that leaves out a predictor that is associated both with outcome and with an included predictor leads to omitted-variable bias. It's even worse in binary regression, as leaving out any outcome-associated predictor inherently leads to bias, even if the omitted predictor is uncorrelated with the included predictors. See this page.

So to continue the answer to the second question, performing separate regressions on each predictor to get separate ROC curves for each predictor is a bad idea. If you really need to have an ROC curve, base it on a complete model that incorporates all predictors together.

With respect to the first question, I don't know that there is a generally reliable way to translate sensitivity and specificity values from an ROC curve to the modeled probability, except in the types of ideal circumstances described by Sextus Empiricus in a comment on the question. If you are going to follow best practice and choose a probability cutoff (if needed) based on relative misclassification costs, you don't need the ROC curve anyway. You just use the probability value that minimizes net cost. The display provided for example by the ROCR package can then show you where that probability lines up on your ROC curve, if you wish.

Finally, one problem with classification tables is that they put too much emphasis on accuracy, sensitivity and specificity, which are not good measures of model performance and ignore the importance of a proper cost-based application of the model. Frank Harrell has written extensively on the problems with such measures; this post is one useful introduction to the issues.

Answer 2

Below is some example data about flowers with

• the category of flower (class 0 or 1)
• the petal width of the flower
• the petal length of the flower

^{connoisseurs might recognize the famous iris data set which I based this example on (I added some jitter and changed the means of the categories)}

What logistic regression does is fit some function that expresses the probability of one of the classes.

^{(the fitting is done by maximum likelihood based on a Bernoulli model for the outcome variable, look it up, or just trust that you get in some way this fit)}

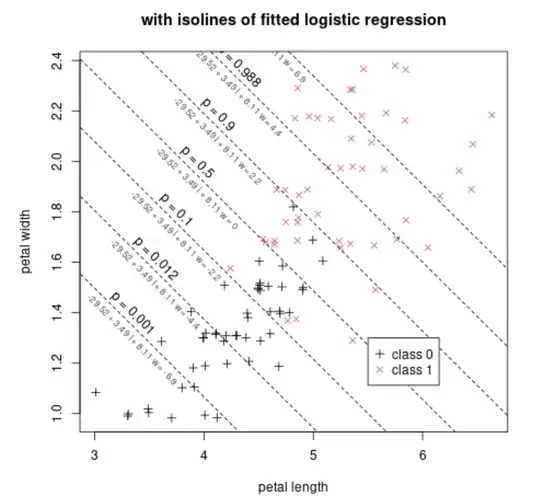
Below we show this function added to the previous scatterplot, by means of isolines. Each isoline represents the places where the below function has the same value

$$p = \frac{1}{1+e^{-b_0 - b_1 \text{length} - b_2 \text{width}}}$$

The fit has found the values $b_0 = -29.52$, $b_1 = 3.49$, $b_2 = 8.11$.

For example the value $p=0.5$ occurs when $b_0 + b_1 l + b_2 w = -29.52 + 3.49 l + 8.11 l = 0$. Along this iso-line $p=0.5$ you see that the presence/density of both classes is roughly equal. Further to the top-right you have more of class 1. Further to the bottom-left you have more of class 0.

We can also make a plot of just this linear predictor $-29.52 + 3.49 l + 8.11 w$ on the x-axis and the probability and the classes on the y-axis.

This might be the graph that you see in many explanations of logistic regression. In your classification the x-axis is a linear combination of all your regressors. In the example that is $-29.52 + 3.49 l + 8.11 w$.

Now, you can choose different cut-off values for this linear predictor. If you place it to the right then you will classify less cases as $1$, and make less false positives, but also less true positives. If you place it to the left then you will classify more cases as $1$, and make more true positives, but also more false positives.

Below is an example of the ROC curve with the example flower data and using the linear classifier based in the logistic regression. On the curve we have drawn several points that relate to the isolines in the plot above.

For example, the point in the upper left corner corresponds with $p=0.5$. This occurs when we classify based on the boundary $-29.52 + 3.49 l + 8.11 w = 0$.

1. Do I simply need to select an X-value from the coordinate table where I have the best sensitivity/specificity (top left corner) and plug it into the formula for P(Y=1)?

The relationship between the ROC coordinates specificity/sensitivity and the value $p$ (or the related linear predictor) is not straightforward.

Especially note that the probability $p$ on the logistic regression is not the same as the false positive rates or true positive rates. And for different cases with the same cutoff $p=0.5$ we can end up with different false positive and false negative rates.

^{For many cases however, the $p=0.5$ corresponds roughly to this upper left corner. This occurs when the two negative and positive classes are distributed with a same symmetrical distribution where only a location parameter differes (e.g. normal distributions with similar covariances).}

But, the ROC curve is often plotted, computed, based on varying the cutoff-value. (That's how I made the graph above, change the cutoff value and for each value compute false/true positive rates). Then, if you select a certain point on the ROC curve for the ideal cutoff, then you can just lookup which cutoff value/criterium created that point on the ROC curve.

2. What do I do when I have more than one predictor (X) variable? Choose the best point/coordinate for both predictors separately and plug in the values into the equation for P(Y=1) and calculate the new cutoff value?

The multiple predictors are combined in a single function and based on that value of that function you determine the classification.

In the example the function is $-29.52 + 3.49 \text{length} + 8.11 \text{width}$ which combines two predictor variables 'length' and 'width' into a single value.

Code for the images:

### some data
set.seed(1)
z = rep(0:1, each = 50)
x = jitter(iris[51:150,3]) - z/4
y = jitter(iris[51:150,4]) - z/8
scatterplot of classes
plot(x,y, pch = 3+z, col = 1+z, xlab = "petal length", ylab = "petal width", main = "example of some data")
legend(5.5, 1.3, c("class 0","class 1"), 
pch = c(3,4), col = c(1,2), bg = "white")
scatterplot of classes
plot(x,y, pch = 3+z, col = 1+z, xlab = "petal length", ylab = "petal width", main = "with isolines of fitted logistic regression")
model
mod = glm(z~x+y, family = binomial)
beta = mod$coefficients
xs = seq(0,10,0.01)
p = c(0.001,0.012,0.100,0.500,0.900,0.988,0.999)
beta
for (pi in p) {
  yp = (-log(1/pi-1) - beta[1] - beta[2]*xs)/beta[3]
  lines(xs,yp, lty = 2)
  sel = which.min((xs-yp-2)^2)
  text(xs[sel],yp[sel]+0.05, paste0("p = ", pi), srt = -45)
  text(xs[sel],yp[sel]-0.05, paste0("-29.52 + 3.49 l + 8.11 w = ", round(-log(1/pi-1),1)), col = rgb(0.3,0.3,0.3), srt = -45, cex = 0.7)
}
legend(5.5, 1.3, c("class 0","class 1"), 
pch = c(3,4), col = c(1,2), bg = "white")
linpred = beta[1] + beta[2]x + beta[3]y
ps = seq(-15,15,0.1)
plot(ps,1/(1+exp(-ps)), xlab = "-29.52 + 3.49 length + 8.11 width", ylab = "probability class 1", type = "l", main = "one dimensional view")
points(linpred, z, pch = 3+z, col = 1+z)
p = seq(0,1,0.01)
falseposrate = c()
trueposrate = c()
for (pi in p) {
  cut = -log(1/pi-1)
  predictions = linpred>cut
  fpr = sum(predictions(1-z))/sum(1-z)
  tpr = sum(predictionsz)/sum(z)
  falseposrate = c(falseposrate,fpr)
  trueposrate = c(trueposrate,tpr)
}
plot(falseposrate,trueposrate, main = "related ROC curve", type = "l",xlim = c(0,1), ylim = c(0,1))
p = c(0.001,0.012,0.100,0.500,0.900,0.988,0.999)
falseposrate = c()
trueposrate = c()
for (pi in p) {
  cut = -log(1/pi-1)
  predictions = linpred>cut
  fpr = sum(predictions(1-z))/sum(1-z)
  tpr = sum(predictionsz)/sum(z)
  falseposrate = c(falseposrate,fpr)
  trueposrate = c(trueposrate,tpr)
}
points(falseposrate,trueposrate, pch = 20)
for (i in 1:7) {
  text(falseposrate[i],trueposrate[i]-0.05, pos = 4, paste0("p = ", p[i]))
#text(falseposrate[i],trueposrate[i] - 0.05, pos = 4, paste0("-29.52 + 3.49 l + 8.11 w = ", round(-log(1/pi-1),1)), col = rgb(0.3,0.3,0.3), cex = 0.7)
}

Answer 3

Thank you so much for all your detailed answers. Even though my question wasn't answered exactly and concisely until the end, I've managed to solve my problem on my own. It was, in essence, quite simple. I always wanted to obtain the cut-off score to use in SPSS; specifically, the predicted probabilities cut-off score. However, I consistently used the raw values variable as the test variable in the ROC curve command, which naturally resulted in cut-off points for raw values only. Now, I've saved the predicted probabilities for my model and used them as the test variable. Consequently, I now have cut-off points for the predicted probabilities in my ROC curve coordinates, which I need to specify for classification in SPSS. Thanks a lot for the numerous responses!