2

So far I have performed an LDA having two classes, but I'm really struggling with certain aspectos of the analysis. I am working with biomedical data in which I would like to classify in k=2 groups: CG and IG based on p = 11 variables. Theorically, as far as I know you're gonna get discriminant functions for k-1 dimmensions and N individuals ( N = 59 in my case).

  1. From the perspective of separation, I've seen graphs explaining two-class discrimination ellipses, I guess coming from centroids. Is this possible? On other posts, I have just seen a density function with a cutoff point discriminating both groups. As I said I am not quite sure about the rule of the two-category group and its display.
  2. Once you perform the lda is there any way from the transformed matrix to infer the weight of the classifiers (p=11).

Thanks in advance!

Javier Hernando
  • 209
  • “Once you perform the lda is there any way from the transformed matrix to infer the weight of the classifiers” Do you mean by 'weights' something else than the parameters in the discriminant function? – Sextus Empiricus Jan 17 '24 at 11:12
  • The influence of the variables. I've read that standardizing variables and then running model. The scaling parameter gives a notion of the influence of variables to discriminate

    data2<- data data2[,2:p_variables] <- scale(data2[,2:p_variables]) lda(class~ . , data2)$scaling

    Am I right about it?

     – Javier Hernando Jan 17 '24 at 11:26
  • Why do LDA rather than logistic regression? I'm not saying your choice is wrong, but I'm wondering about it, since LDA has more assumptions than logistic reg. does (e.g that the data are normally distributed). – Peter Flom Jan 17 '24 at 11:43
  • Data is normally distributed. Not sure about it, I'm comparing it with PCA, and as far as I know both PCA and LDA seem to complement each other, plus I was interested in observing if the set of variables selected could be able to classify correctly, and I kind of understood this is more about LDA. To be honest I don't totally understand difference between the 2 methods to give a coherent answer on why picking one over the other – Javier Hernando Jan 17 '24 at 11:51
  • LDA leads to a logistic function for class probabilities: https://stats.stackexchange.com/questions/549508/ However it is not the same procedure as logistic regression. Logistic regression can occur in other ways as well (e.g. as approximation for a probit model with completely different distributions than the multivariate normal distribution). The fitting procedure differs. LDA fits the the underlying latent model (the multivariate normal distributions). I imagine that LDA might perform better than logistic regression when the assumptions are true (because it uses more information). – Sextus Empiricus Jan 17 '24 at 12:02
  • Other links for the logistic function: https://stats.stackexchange.com/questions/597031/ – Sextus Empiricus Jan 17 '24 at 12:09

1 Answers1

0

I've seen graphs explaining two-class discrimination ellipses, I guess coming from centroids.

...

On other posts, I have just seen a density function with a cutoff point discriminating both groups.

Both situations apply to a two-class LDA.

Bayes classifier

You can consider LDA as a Bayes classifier, assuming multivariate Gaussian distributions for the classes.

An example image that shows how this works is:

(I have to find a better one, this image here fits distributions with different covariance, and the QDA curve is the result, the LDA curve has been added for comparison)

You can see the elipses which are the fitted densities for the two distributions. and the points where they have the same value P(class 1) = P(class 2) is the classifier boundary.

example

One dimensional viewpoint

For the LDA the classifier is a single p-1 dimensional plane and we can consider a coordinate that is along the normal vector on that plane.

An analogues switch to a 1 dimensional vector is made here for logistic regression: Probability threshold in ROC curve analyses

We have some distribution of variables for two classes. Below this is shown for two variables, such that we can plot it, but the principle is the same in higher dimensions.

example data

To this we fit a linear classifier that represents several parallel iso-planes in the space. At each plane we predict a certain odds or probability ratio P(class 1)/P(class 2)

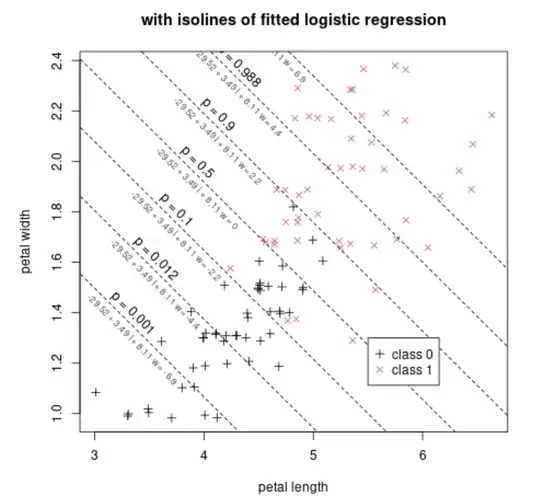
with additional logistic function isolines

This data can be projected onto a single dimension that is perpendicular to those planes, and then we have a 1-dimensional view like below.

one dimensional view

The picture above is a typical image for logistic regression, plotting the single observed points, but the points can also be represented as a density (using a histogram or some estimation of the density)

An example is the graph below (now with three classes):

From "The use of multiple measurements in taxonomic problems" Annals of Eugenics, Vol VII, Pt. II, op. 179-188, 136

example of distribution for projection of iris data

Another graph that might help to see the connection between the multidimensional centroids and the 1-dimensional density graphs is:

The histograms show the distribution of the two classes along different 1 dimensional directions.

example iris

Sextus Empiricus
  • 77,915
  • I don't truly understand which parameters are you going to use for depicting the ellipses. The origin is not methodologically specified. The standardized coefficients? I am just getting one column. The posterior probabilities? About the image similar to logit regression, the coefficients you get assure 100% discrimination such as depicted? Probability class 1 completely distinguished from class 0? I guess this has something to do with the graph of isolines which I don't know its meaning either. – Javier Hernando Jan 17 '24 at 14:42
  • "I don't truly understand which parameters are you going to use for depicting the ellipses" In the example I used 2 parameters, such that it can be plotted, but more generally these ellipses are multidimensional and use all parameters. – Sextus Empiricus Jan 17 '24 at 19:55
  • What does it mean all parameters? Scores? Standardized coefficientes? – Javier Hernando Jan 18 '24 at 08:22
  • @JavierHernando sorry I mix these terms up often. I mean variables. In the example of the answer I depicted a scatter plot with 2 variables. In computations this can be all of your 11 variables. – Sextus Empiricus Jan 18 '24 at 11:47