How to create a loss function to reflect different costs of misclassification errors?

Question

I am currently reading 'Pattern Recognition and Machine Learning' and came across an example of a confusion matrix comparing the actual vs predicted number of people with or without cancer.

The penalty/loss is due to a misclassification: If you ACTUALLY have cancer but is classified by the algorithm as "healthy", then this is extremely bad. Another misclassification is not as 'gravely' erroneous as actually being "healthy" despite having been misclassified as "having cancer" by the algorithm.

My question is: For a logistic regression, how do you create/formulate a loss function that can capture the essence of penalising 'different levels of errors'?

Which loss function? The ordinary logistic regression loss function doesn’t distinguish between types of errors, which you can verify by inspection. Instead, there is a penalty for a prediction far away from the label, and this penalty grows as the distance from the correct label increases. Additionally, the ordinary logistic regression function is not regularized, so it's not clear what function or usage you're asking about. — Sycorax, Mar 09 '21 at 03:37
@Sycorax Can you kindly give an example for this? for logistic regression? — cgo, Mar 09 '21 at 03:47
Example of what? The passage in Bishop is just describing the concept that the costs of different kinds of classification errors are not equal. There's nothing in that passage that connects the inequality of error costs to the loss function of logistic regression. — Sycorax, Mar 09 '21 at 03:50
@Sycorax exactly my point. So if this were a classification task using logistic regression, how would you formulate a loss function to incorporate this idea of different losses. — cgo, Mar 09 '21 at 04:09
You'll need to edit your question to clarify that this is what you want to know — Sycorax, Mar 09 '21 at 04:11

score 1 · Answer 1 · answered Jul 25 '23 at 21:12

I highly suggest reading this answer:

https://stats.stackexchange.com/a/312787/97124

You want your logistic regression model to accurately represent the probability of getting cancer as a function of your independent variables. Using this model to make a classification decision should be a distinct step. Often it is inappropriate to use the "default" threshold of $0.5$ for your classification step. You need to make an analysis of the consequences of false negatives, false positives, etc.

Maybe you could specify a utility function of some sort (what is the utility of a true positive, true negative, false positive, false negative) and optimize the total utility as a function of the threshold?

score 0 · Answer 2 · answered Mar 09 '21 at 04:56

0

In the setting of logistic regression, though not in general, you can optimise with different penalties for the two possible errors simply by adjusting the intercept ('bias') term or equivalently by adjusting the decision threshold.

That is, if $$\mathrm{logit}\, {P(Y=1|X=x)}= \alpha+\beta x$$ with a threshold of $p$ is optimal for equal loss, and you want losses of $a$ for false positives and $b$ for false negatives, you can set $ \alpha\mapsto \alpha+\log(b/a)$, or make the equivalent change to $p$.

Strictly speaking, this is only true if the logistic regression model is correctly specified, but it's a good approximation.

answered Mar 09 '21 at 04:56

Thomas Lumley

38,062

"this is only true if the logistic regression model is correctly specified" I believe that this method does not work, also for a correctly specified model. The probability parameter that the logistic model uses is not the same as the false positive rate or true positive rate. Different models with the same parameter can have different false positive rate and true positive rate. See Is it possible to adjust a logistic regression model when the false positive rate is too high for observations belonging to a specific category?. – Sextus Empiricus Dec 28 '23 at 15:18

Sextus Empiricus · Answer 3 · 2023-12-28T15:37:18.213

The logistic regression does not fit classes but instead probabilities. The log loss for a single data point is

$$L = \begin{cases} \log(\hat{p}_i)& \qquad \text{if $y=1$} \\ \log(1-\hat{p}_i) &\qquad \text{if $y=0$} \\ \end{cases}$$

where $\hat{p}$ is the fitted estimate.

If you change this with some parameter like

$$L = \begin{cases} w_i\log(\hat{p}_i)& \qquad \text{if $y=1$} \\ \log(1-\hat{p}_i) &\qquad \text{if $y=0$} \\ \end{cases}$$

then this is similar to adding different weights to the cases with $y=1$.

Changing the loss function for fitting like this, is probably not gonna improve your results. The loss function used for the fitting needs to reflect the statistical model in order to make an estimate with a small error (to be efficient). You can use a second additional loss function in validation of the model and tweak the model based on the outcome of that second validation. The loss function in fitting is used to reduce error from statistical variations, the loss function in validation is used to reduce error/costs from model bias. (See also: Could a mismatch between loss functions used for fitting vs. tuning parameter selection be justified?)

For a logistic regression you can use a validation data set that you use to define a classification boundary and classification rules like

$$\text{'class 1 if $\hat{p}> p_c$'}\\ \text{'class 0 if $\hat{p} \leq p_c$'}$$

and optimize $p_c$ based on false positive and false negative rates in the validation data.

You can also possibly do this without a validation data set and compute false positive and false negative error rates based on the data used for fitting.

This procedure can look like the graph below occuring in this question: Are non-crossing ROC curves sufficient to rank classifiers by expected loss?

The graph shows an ROC curve, and superposed are isolines for the values of a cost function as function of the false and true positive rates.

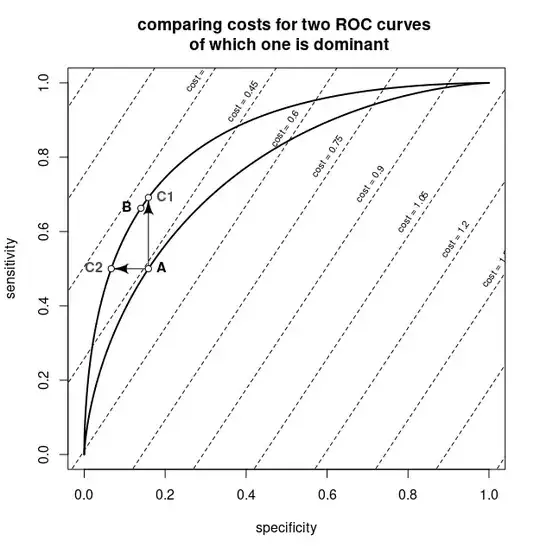
An example how such ROC curve stems from logistic regression is explained in Probability threshold in ROC curve analyses. The curve is like a parametric curve that is a function of $p_c$ and will look as something like the figure below.

If the model is not correctly specified (and the statistical fit based on likelihood will not function well) then it might be an interesting idea to fit a model by searching for a linear function as a classification boundary that only predicts the classification and not a value $p$. That is, optimize a linear function $X\beta$ such that we minimize

$$Cost =\begin{cases} a & \quad \text{false positive $X\beta >0$ and $y=0$} \\ 0 & \quad \text{true negative $X\beta <0$ and $y=0$} \\ 0 & \quad \text{true positive $X\beta >0$ and $y=1$} \\ b &\quad\text{false negative $X\beta <0$ and $y=1$} \\ \end{cases}$$

How to create a loss function to reflect different costs of misclassification errors?

3 Answers3