I just read that SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model
Can anybody please help me to understand that what is the importance of alpha, beta, rho in the SABR volatility model?
We created the SABR model because we realized that (a) option values were nonlinear in the volatility, and (b) volatilities are stochastic. This means that if one had an option (or portfolio of options) which have positive gamma in the volatility dimension, on average we'd make money from fluctuations in the volatility, and we'd lose money with negative vol-gamma. To be fair, these gains or losses should be compensated for in the daily carry ... it's just Black Scholes in the volatility dimension. We created the model so that we wouldn't leak money due to the volatility of the volatility. It turns out that at-the-money options are nearly linear in the volatility, so there is little vol-gamma for ATM options, and much higher levels of vol-gamma for options away from the money ... so the SABR price correction is much stronger away from the money, resulting in a volatility smile. Pat
Alpha, Beta and Rho are the point of the model. So explaining them is explaining the model.
Unlike earlier models in which the volatility was modelled as a constant (Vasicek, Hull-White, etc), SABR assumes that as well as the price of the thing being stochastic, so is its volatility. That is, the volatility will also follow some stochastic path.
Thus we have two clearly related processes; the price, lets say of a forward rate (following the Wikipedia notation):
$$dF_t = \sigma_t F_t^\beta dW_t$$
Which just means the changes in the price are proportional to the price itself raised to power $\beta$, and a Wiener process $W_t$, scaled by the now time-dependent volatility $\sigma_t$.
We also have a process for the volatility $\sigma_t$:
$$d\sigma_t = \alpha \sigma_t dZ_t$$
Again, the changes in volatility are proportional to the volatility itself (so the behaviour is scale invariant) and to a second Wiener process $Z_t$, all scaled this time by $\alpha$.
$\alpha$ is then the (constant) volatility of the volatility. I mean, we could model that as stochastic too but that seems like hard work.
$\alpha$ was the volvol, $\beta$ was the power in the price relation, we are missing $\rho$.
Since the two processes (the price and its volatility) are very much related, the SABR model connects the two Wiener processes driving their movement by making them correlated with parameter $\rho$:
$$dW_t dZ_t = \rho dt$$
So changes in the two Wiener processes are correlated with $\rho$ in time. Again, $\rho$ is a constant.
So none of $\alpha$, $\beta$ or $\rho$ are stochastic; perhaps the name should have been Stochastic Volatility, Alpha Beta Rho. But SVABR is much less catchy.
Ah yes. While the market does quote volatilities, it doesn't quote these parameters, so it's hard to just knit a model in Excel and wear it.
The equations we have so far model the dynamics given the parameters, so in order to get the parameters we will have to essentially solve for the parameters given some other stuff, like market prices for options which are sensitive to those parameters.
Calibrating a set of parameter values to market quotes is the subject of much effort, e.g. this blog post.
No model is able to magically capture all the information available, and there would be no point; a model's power is in deriving simpler truths than the information you start with. With SABR the model better recreates the dynamics of the evolution of an interest rate, but note that there are just a small, fixed number of parameters. So it cannot calibrate perfectly to a market with tens or hundreds of inputs.
Unless I am missing the obvious, I do not see the question being answered? In my opinion, trying to understand in simple language what $\alpha, \beta, \rho$ mean requires an explanation what these parameters do and why it is useful.
Here is my attempt: Black (all Black Scholes formulas) assume(s) that Implied Volatility is independent of strike (constant and known). However, this is usually not the case and if you plot (quoted) IVOL and strike, you see what is called a smile or skew. SABR can be used to interpolate (and extrapolate) a vol smile.
Before talking about SABR, let us consider $\beta$ separately. The CEV model does not assume a lognormal (Black) process but is more general: $$dF = \alpha * F ^ \beta * dW$$ where $\alpha$ corresponds to the CEV volatility (sets the overall level of volatility), $\beta$ is the CEV parameter (which determines the skew) and $W$ is Brownian motion.
Now, in terms of what level, skew and smile actually mean or look like, I recommend to have a look at this illustration in the FX market. The level will be what is shown as the flat vol for all strikes (simple ATM only), skew is the CEV parameter. For $\beta < 1$, the vol smile is a decreasing function of the strike price. A major problem is that it is not able to produce a smile (the upward sloping wings in the FX example I linked).
That is where SABR comes in: On top of CEV, the new assumption is that volatility is not constant as it is in CEV but a stochastic process itself. Hence, $\sigma$ itself is governed by an SDE, just like the forward rate (as assumed in Black and CEV). The two Brownian motions (for forward rate and vol) are correlated through correlation coefficient $\rho$.
How to get or set $\beta$ is explained here. This answer shows how $\beta$ can be estimated and what the effect and interpretation of $\beta$ are.
Once you have $\beta$,
The gif below uses Julia and the formulas 2.17 onwards, starting on P.89, of Managing Smile Risk. Wilmott, 1, 84-108,.
# load packages
using Plots, PlotThemes, Interact, LaTeXStrings
theme(:juno)
#define inputs
β, α, ρ, ν, t_ex, f1, f2, f3, t_ex = 1, 0.05, 0, 1, 1, 0.03, 0.05, 0.07, 1
K = 0.01:0.0001:0.1
#define the expression
function σ_b(β,α, ρ, ν, t_ex, f, K)
A = α /(((fK)^((1-β)/2))(1+((1-β)^2)/24log(2,(f/K))+ ((1-β)^4)/1920log(4,(f/K))))
B = 1+(((1-β)^2)/24(α^2/(fK)^(1-β))+(1/4)αβρν/((fK)^((1-β)/2))+(2-3ρ^2)/24ν^2)t_ex
z = ν/α(fK)^((1-β)/2)log(f/K)
χ_z = log((sqrt(1-2ρz+z^2)+z-ρ)/(1-ρ))
atm = α/(f^(1-β))(1+(((1-β)^2)/24(α^2/(fK)^(1-β))+(1/4)αβρν/((fK)^((1-β)/2))+(2-3ρ^2)/24ν^2)t_ex)
cond = f==K
return cond ? atm : Az/χ_zB, atm
end
define plots
plot(K,[x[1] for x in σb.(β,α, ρ, ν, t_ex, f, K)], size =(800,500), margin=5Plots.mm,
title = "SABR Model \n(β = $β, α = $α, ρ = $ρ, ν = $ν, "L"$ t{ex}"" = $t_ex)",
label = "f = $(round((f100),digits=1))%",
xlabel = "Strikes",
ylabel = "Volatility")
ylims!((0, ylims()[2]+ylims()[1]))
vline!([f], label = "ATM vol = $(round(minimum([x[2] for x in σ_b.(β,α, ρ, ν, t_ex, f, K)]),digits = 2))")
ylims!((0,maximum(x[1] for x in σ_b.(β,α, ρ, ν, t_ex, f3, K))))
xlims!((minimum(K),maximum(K)))
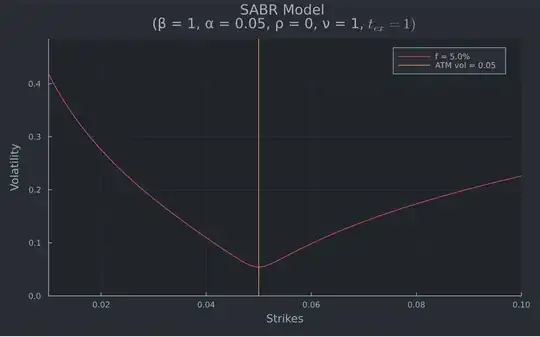
Adding a few lines similar to this answer makes the chart interactive.
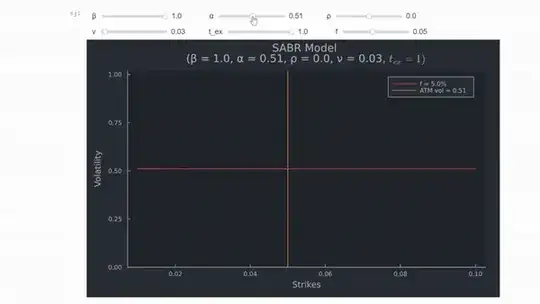
Changing the level of correlation makes the smile "rotate" around the ATM point, and if $\rho < 0$, volatility is lower for higher (ITM) strike prices and vice versa (vol increases on the left-hand side of the figure).
Therefore, it is possible to fit the entire vol curve nicely with this model. One side remark, it will NOT fit quoted vols as it is a general best fit around all points. If matching quoted vols is a desired feature, one could for example combine piecewise linear within quoted spectrum and SABR for extrapolation.
Edit:
I followed the notation on P.13 of the original paper which states that
The three parameters α, ρ and ν have different effects on the curve: the parameter α mainly controls the overall height of the curve, changing the correlation ρ controls the curve’s skew, and changing the vol of vol ν controls how much smile the curve exhibits.
The other answer (by the way, refering to the answer above me is misleading because you can sort the answers in several ways) uses the notation from Wikipedia it seems. Wikipedia defines α as $\sigma$ and ν as α, which is quite misleading, given the choice of parameters in the original paper. Also, the authors (see the paper on P.8) chose the name "stochastic-αβρ model", which has become known as the SABR model because they make α (the volatility) a stochastic process. That's also something the other answer clearly missed it seems.
The are implied parameters. You basically do a parametric dimension reduction by implying them across a range of observed prices, checking the errors, and then you might interpolate or even cautiously extrapolate. In reality, desks will have their own spreads but you can generate a volatility surface as a baseline from these parameters.
If I remember correctly, there might be some issues with this parametrization in terms of stability depending on what you are doing.
