How should we do boxplots with small samples?

Question

This question is inspired by this posting, plus a comment by @StephanKolassa and an answer by @dipetkov who point out that the boxplots presented in that question are misleading. As is pointed out, boxplots display 5 summary statistics (the minimum, lower quartile, median, upper quartile, and maximum) of a sample; but in some instances, the sample size was only 2. It seems ridiculous to try to construct a 5-number "summary" of a sample of size 2. On the other side of the coin, if we have a sample of 100 observations, a boxplot clearly displays a summary of the data.

This led me to want to investigate what is done by popular R functions for constructing boxplots. Hence the example below for a simulated dataset with three groups and sample sizes 2, 5, and 15 respectively.

set.seed(42)
foo = data.frame(group = rep(1:3, c(2, 5, 15)), 
                 y = c(rnorm(2, mean = 2), rnorm(5, mean = 0), 
                       rnorm(15, mean = 1)))
standard graphics
boxplot(y ~ group, data = foo)

# lattice graphics
library(lattice)

bwplot(~ y | group, data = foo)

# ggplot2 graphics
library(ggplot2)
ggplot(data = foo, aes(factor(group), y)) + geom_boxplot()

^{Created on 2022-07-19 by the reprex package (v2.0.1)}

What we see is that in all three graphics methods -- standard, lattice, and ggplot -- the software glibly produces boxplots for all three groups.

So my question is

1. Is it appropriate that boxplot software should construct a boxplot regardless of the sample size?
2. If not, what should it do instead?

Answer 1

I believe that this is a case where software misleads users. So my answer to (1) is "no." When we try to "summarize" a sample of 2 values, or even 5, with a display containing 5 elements, that can only be classed as a distortion, not a summary. The goal of statistical methods is to clarify, not obfuscate; so I think the software examples we see here are actually harmful to statistical practice.

For question (2), a very simple alternative is to simply plot the points instead of the boxplot when the sample size is small. Such a one-dimensional scatterplot (or dotplot) fits on the same scale as the boxplot, so such a solution does not create any complications in the graphical layout. Nor does it complicate a user's interpretation because it is self-explanatory.

I think a decent boxplot routine should implement a threshold below which a 1-dimensional scatterplot is produced instead of a box. I suggest the default threshold be at $n = 8$ or $n = 10$. Moreover some care should be taken (say, by offsetting points in the perpendicular direction of the scale) to ensure that every one of points is visible when there are overlapping values. This should be simple, given that only a small number of values is involved.

Appendix

Here is a hack for the standard graphics function:

guts = boxplot(y ~ group, data = foo, plot = FALSE)
guts$stats[,1] = guts$stats[3,1]
guts$stats[,2] = guts$stats[3,2]
guts$out = foo$y[1:7]
guts$group = foo$group[1:7]
bxp(guts, main = "Alternative boxplots", ylab = "y", xlab = "group")

This made all 5 numbers of the 5-number summary equal to the median for the first two groups, and designated as outliers all the data values for those groups. Put another way, the box heights and whisker lengths for the small-data groups are set to zero, and all the values are regarded as outliers. I think this is a much more acceptable way to present those first two groups.

Answer 2

What R implementations (should) do is for developers and users of that software. I wish to comment more broadly on limitations of box plots.

This overlaps a little with points made in other answers, and I am happy to note agreements. But at the risk of some repetition I wanted this answer to seem coherent, at least to me.

Box plots as known at present owe most to a re-invention by J.W. Tukey in the 1970s (most visibly in Exploratory Data Analysis, 1977) of dispersion diagrams used by geographers routinely from the 1930s, which in turn were channelling an idea stretching back through A.L. Bowley to Francis Galton that (in modern terms) plots, or more generally reports on data, that were based on particular quantiles could give useful summaries and helpful detail as well.

This history is poorly understood, partly because few non-geographers are well read in geographical literature, although Tukey himself was aware of it. The meme that Tukey invented box plots is at best supplemented by an unhistorical mention of Marion E. Spear on range-bar plots. Spear herself was using but not citing earlier work by Kenneth W. Haemer, which itself ignored geographical predecessors, and Bowley, and Galton. But no one can be expected to know about all previous uses of statistical graphics anywhere.

The precursors of box plots in many cases showed much more detail than bare box plots do, often all data points. In contrast, the focus of Tukey's work on box plots was whatever could be done quickly with pen and paper alone, with some expectation that a user was able and willing to do some simple calculations, such as averaging two numbers or multiplying by 1.5. As someone aged 25 in 1977, I still benefit from years of schooling in "mental arithmetic" (no workings on paper allowed, let alone slide rules or calculators or any other aid) as well as "mechanical arithmetic" (working on paper allowed). This is almost never anyone's routine situation with data analysis 50 years later. Further, the aim of a box plot was mostly exploratory, for example to identify data points that need thinking about, and possibly some action such as a transformation.

Tukey himself would never have defended the box plot as fit for all kinds of data. Problem areas include, and are not limited to,

1. Very small samples, as in the question.

2. Discrete outcomes (e.g. counted or categorical data). For example, there are many threads here arising from puzzlement when either whisker is not shown or some other element of a box plot is apparently missing. The data don't have to be pathological or bizarre to produce a weird-looking box plot that is hard for many newcomers to decode. For example, suppose 60% of values are 0, 30% of values are 1, 10% of values are 2. Then the minimum, lower quartile and median coincide, the IQR is 1 and the 2s just show implicitly at the end of one whisker. Now suppose 80% of values are 0.....

3. U-shaped distributions. Tukey gave an example of Rayleigh's data (which led to the discovery of argon) which fall in two clumps, so that the box is long and the whiskers short. Beyond that, long boxes and short whiskers are often misinterpreted as distributions with short thin tails too, people forgetting that if 50% of the distribution is inside the box, then 50% is outside, and the average density outside the box can be (much) higher.

In all these cases, there are simple ripostes, to use something else instead or to think a little harder (or to provide a better story).

As far as the question is concerned:

• Programmers (me too in other contexts) need to think about what is the default behaviour of their programs. I wouldn't recommend a threshold sample size below which the box plot is ignored and something else is done. I might recommend an option to do that.

• As above, most of the difficulties are avoided by plotting box plots routinely with some other representation juxtaposed or superimposed, either a dot or strip plot or a quantile plot (or occasionally a histogram). There are many variants of this idea already. The most popular seem based on jittering otherwise identical data points apart. I favour stacking in some sense, as jittering isn't so easy to decode in terms of a local density.

Here is an example in the same spirit as the question.

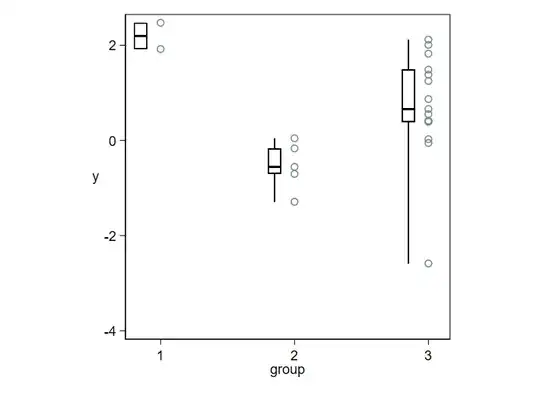
So long as data points are shown directly, it becomes trivial to decode puzzling box plots, or to ignore them as unhelpful. With larger samples, not the question but clearly important too, you can use most of the space for direct representation of the data and let the box plots be thin summaries.

Detail: If you show all the data, the need to follow rules like "Plot data points individually whenever any is more than 1.5 IQR from the nearer quartile" diminishes, if it doesn't disappear. Such rules are in any case routinely not well explained, not well understood, or both. So, the whiskers can just extend to the extremes, or (as is quite often done) you can just have the whiskers extend to say the 5% and 95% points, so long as you explain your convention.

The stark contrast between thick box and thin whiskers that is conventional overstates the importance of quartiles as thresholds or even as summaries. Naturally, this is familiar to anyone preferring a density plot or even a histogram.

With this style there is no need to vary box width, as different group sizes are shown by the number of data points. It is often helpful in any case to add text of the form $ n = 15$ at some convenient place.

As a further signal of possibilities, consider this design for a larger dataset in which tied data values make essential either stacking (as here) or jittering (if you prefer) if you want to see the detail of all data points. The box plot here is a box plot without a box and based on a 1983 suggestion by Edward R. Tufte. He called the design a quartile plot. Others have used the term midgap plot. The name is unimportant except for Googling mentions. Tufte's original goal seems most of all a minimal display using as little ink as possible. I too like its minimalism, but suggest a more statistical motive: it helpfully shifts emphasis from middles to tails. Often, if not most often, what is going on in the tails is as or more important to track as is what is going on in the middles of distributions. I use a marker or point symbol for the median that is more prominent than the point symbols used by Tufte. Minimalism like almost any other virtue can be carried to excess.

Ironically, or otherwise, in his 2020 book Tufte comes out against this earlier design and enjoins showing the data in detail. But as I do that too with this hybrid design I feel no guilt on that score.

Answer 3

This question touches on the intersection of statistics and software engineering. The statistical part of the question is uncontroversial: the boxplots, like many other statistics and data visualization methods, don't have much sense below some sample size. The software engineering part is more tricky and less obvious. There are many possible solutions, each with its pros and cons:

• You could do nothing as it happens right now in the examples. One of the important software design principles is the principle of least surprise, to avoid the wat! moments, summarised here as

  Simply put, this principle holds that a given operation’s result should be, “obvious, consistent, and predictable, based upon the name of the operation and other clues.”

  The "boxplot" function ought to create a boxplot, so it should create a boxplot, not more, not less. Producing the plot in such a case leads to garbage-in, garbage-out result. We are letting the user shoot themselves in a foot if that is what they want to do. I agree with you that the above is not the most pretty solution. On another hand, it acknowledges the fact that users may be using your software in hard to foresee ways (e.g. to create teaching examples “how not to make boxplots”).

• If we want to be slightly more empathetic with the user, we can warn them that what they are trying to do is not the best thing to do.

• If we decide that we cannot produce a plot for the small sample size, we can fail with an error. This is consistent with the idea of failing fast.

  Imagine you are auto-generating a report. Due to a bug in your code, you accidentally pass a smaller sample than intended to the boxplot function. If the function has some special handling of such cases (e.g. producing a different plot) the problem may end up undetected, or you might be wasting a lot of time on debugging the reason why the plot is not what you expected. (The same thing happens when you choose the "do nothing" approach.)

• Another solution is for the function to run in degraded mode in case of insufficient data. We can't produce a boxplot, but we can show something like a degraded boxplot, for example with three points showing only the minimum, maximum, and the mode (the elements of boxplot), or show all of the points as outliers. With more points, but still not enough for a boxplot, you could add some other elements if sufficient. Again, you can (if not should), combine this with a warning.

• Finally, you could produce a different plot for such data. I'd say, this falls into the realm of failing silently, which is an anti-pattern in general.

Answer 4

I consider the question "What's the smallest sample size for which a box-and-whiskers plot is a useful visual summary" to be about a rule-of-thumb for making good plots. (The question "Should implementations of a box-and-whiskers plot enforce a minimum sample size" does seem to be about opinions rather than practice.)

I looked for advice in a few books about statistical graphics. It seems straight advice is hard to find. So far I have:

[1] J. Tukey. Exploratory Data Analysis (1977)

First a general comment on page 29:

If we are to select a few easily-found numbers to tell something about a batch as a whole, (...) we would like these values to be easy to find and write down, whether the total count of the batch is 8, or 82, or 208.

And more specifically about boxplots, which Tukey calls schematic plots, in reference to visualizing 15 weight measurements from a 1893-94 experiment by Lord Rayleigh:

Here the main issue (...) is made quite clear by the individual values of the dot plot--and almost completely covered by the schematic plot. (Only almost, because the experienced viewer--finding the whiskers so short, in comparison with the box length--is likely to become suspicious that he should see more detail.)
Clearly we cannot rely on schematic plots to call our attention to structure near the center of the batch (...)
Exhibit 11 uses the schematic plots for one of the purposes for which they are best fitted: comparison of two or more batches. In it, the two batches of Rayleigh's weights (one batch of 7 from air and another batch of 8 from other sources) are set out and compared.

[2] F. J. Anscombe. Graphs in statistical analysis. The American Statistician, 27(1):17–21, 1973.

Each datasets in the famous quartet has 11 points, so Anscombe's implicit advice is to not summarize fewer than 12 points?

---

Summary: John Tukey suggests indirectly to have at least 8 points for a box-and-whishers plot. He also has a hint about catching out a misapplied boxplot.

Answer 5

Just curious -- Looking outside of R with the same data...

Stata

SPSS

SAS Enterprise Guide

MATLAB (Statistics and Machine Learning tools)

Minitab

I was most curious about Minitab, but our virtual desktop access seemed to require a license. I'd be curious if somebody could fill this one in...

Summary

I see lots of different styles, some I like a whole lot better than others, but all programs tested were happy to make boxplots with 2 data values.