Is there any good reason to use PCA instead of EFA? Also, can PCA be a substitute for factor analysis?

Question

In some disciplines, PCA (principal component analysis) is systematically used without any justification, and PCA and EFA (exploratory factor analysis) are considered as synonyms.

I therefore recently used PCA to analyse the results of a scale validation study (21 items on 7-points Likert scale, assumed to compose 3 factors of 7 items each) and a reviewer asks me why I chose PCA instead of EFA. I read about the differences between both techniques, and it seems that EFA is favored against PCA in a majority of your answers here.

Do you have any good reasons for why PCA would be a better choice? What benefits it could provide and why it could be a wise choice in my case?

Answer 1

Disclaimer: @ttnphns is very knowledgeable about both PCA and FA, and I respect his opinion and have learned a lot from many of his great answers on the topic. However, I tend to disagree with his reply here, as well as with other (numerous) posts on this topic here on CV, not only his; or rather, I think they have limited applicability.

---

I think that the difference between PCA and FA is overrated.

Look at it like that: both methods attempt to provide a low-rank approximation of a given covariance (or correlation) matrix. "Low-rank" means that only a limited (low) number of latent factors or principal components is used. If the $n \times n$ covariance matrix of the data is $\mathbf C$, then the models are:

\begin{align} \mathrm{PCA:} &\:\:\: \mathbf C \approx \mathbf W \mathbf W^\top \\ \mathrm{PPCA:} &\:\:\: \mathbf C \approx \mathbf W \mathbf W^\top + \sigma^2 \mathbf I \\ \mathrm{FA:} &\:\:\: \mathbf C \approx \mathbf W \mathbf W^\top + \boldsymbol \Psi \end{align}

Here $\mathbf W$ is a matrix with $k$ columns (where $k$ is usually chosen to be a small number, $k<n$), representing $k$ principal components or factors, $\mathbf I$ is an identity matrix, and $\boldsymbol \Psi$ is a diagonal matrix. Each method can be formulated as finding $\mathbf W$ (and the rest) minimizing the [norm of the] difference between left-hand and right-hand sides.

PPCA stands for probabilistic PCA, and if you don't know what that is, it does not matter so much for now. I wanted to mention it, because it neatly fits between PCA and FA, having intermediate model complexity. It also puts the allegedly large difference between PCA and FA into perspective: even though it is a probabilistic model (exactly like FA), it actually turns out to be almost equivalent to PCA ($\mathbf W$ spans the same subspace).

Most importantly, note that the models only differ in how they treat the diagonal of $\mathbf C$. As the dimensionality $n$ increases, the diagonal becomes in a way less and less important (because there are only $n$ elements on the diagonal and $n(n-1)/2 = \mathcal O (n^2)$ elements off the diagonal). As a result, for the large $n$ there is usually not much of a difference between PCA and FA at all, an observation that is rarely appreciated. For small $n$ they can indeed differ a lot.

Now to answer your main question as to why people in some disciplines seem to prefer PCA. I guess it boils down to the fact that it is mathematically a lot easier than FA (this is not obvious from the above formulas, so you have to believe me here):

1. PCA -- as well as PPCA, which is only slightly different, -- has an analytic solution, whereas FA does not. So FA needs to be numerically fit, there exist various algorithms of doing it, giving possibly different answers and operating under different assumptions, etc. etc. In some cases some algorithms can get stuck (see e.g. "heywood cases"). For PCA you perform an eigen-decomposition and you are done; FA is a lot more messy.

   Technically, PCA simply rotates the variables, and that is why one can refer to it as a mere transformation, as @NickCox did in his comment above.

2. PCA solution does not depend on $k$: you can find first three PCs ($k=3$) and the first two of those are going to be identical to the ones you would find if you initially set $k=2$. That is not true for FA: solution for $k=2$ is not necessarily contained inside the solution for $k=3$. This is counter-intuitive and confusing.

Of course FA is more flexible model than PCA (after all, it has more parameters) and can often be more useful. I am not arguing against that. What I am arguing against, is the claim that they are conceptually very different with PCA being about "describing the data" and FA being about "finding latent variables". I just do not see this is as true [almost] at all.

To comment on some specific points mentioned above and in the linked answers:

• "in PCA the number of dimensions to extract/retain is fundamentally subjective, while in EFA the number is fixed, and you usually have to check several solutions" -- well, the choice of the solution is still subjective, so I don't see any conceptual difference here. In both cases, $k$ is (subjectively or objectively) chosen to optimize the trade-off between model fit and model complexity.

• "FA is able to explain pairwise correlations (covariances). PCA generally cannot do it" -- not really, both of them explain correlations better and better as $k$ grows.

• Sometimes extra confusion arises (but not in @ttnphns's answers!) due to the different practices in the disciplines using PCA and FA. For example, it is a common practice to rotate factors in FA to improve interpretability. This is rarely done after PCA, but in principle nothing is preventing it. So people often tend to think that FA gives you something "interpretable" and PCA does not, but this is often an illusion.

Finally, let me stress again that for very small $n$ the differences between PCA and FA can indeed be large, and maybe some of the claims in favour of FA are done with small $n$ in mind. As an extreme example, for $n=2$ a single factor can always perfectly explain the correlation, but one PC can fail to do it quite badly.

---

Update 1: generative models of the data

You can see from the number of comments that what I am saying is taken to be controversial. At the risk of flooding the comment section even further, here are some remarks regarding "models" (see comments by @ttnphns and @gung). @ttnphns does not like that I used the word "model" [of the covariance matrix] to refer to the approximations above; it is an issue of terminology, but what he calls "models" are probabilistic/generative models of the data:

\begin{align} \mathrm{PPCA}: &\:\:\: \mathbf x = \mathbf W \mathbf z + \boldsymbol \mu + \boldsymbol \epsilon, \; \boldsymbol \epsilon \sim \mathcal N(0, \sigma^2 \mathbf I) \\ \mathrm{FA}: &\:\:\: \mathbf x = \mathbf W \mathbf z + \boldsymbol \mu + \boldsymbol \epsilon, \; \boldsymbol \epsilon \sim \mathcal N(0, \boldsymbol \Psi) \end{align}

Note that PCA is not a probabilistic model, and cannot be formulated in this way.

The difference between PPCA and FA is in the noise term: PPCA assumes the same noise variance $\sigma^2$ for each variable, whereas FA assumes different variances $\Psi_{ii}$ ("uniquenesses"). This minor difference has important consequences. Both models can be fit with a general expectation-maximization algorithm. For FA no analytic solution is known, but for PPCA one can analytically derive the solution that EM will converge to (both $\sigma^2$ and $\mathbf W$). Turns out, $\mathbf W_\mathrm{PPCA}$ has columns in the same direction but with a smaller length than standard PCA loadings $\mathbf W_\mathrm{PCA}$ (I omit exact formulas). For that reason I think of PPCA as "almost" PCA: $\mathbf W$ in both cases span the same "principal subspace".

The proof (Tipping and Bishop 1999) is a bit technical; the intuitive reason for why homogeneous noise variance leads to a much simpler solution is that $\mathbf C - \sigma^2 \mathbf I$ has the same eigenvectors as $\mathbf C$ for any value of $\sigma^2$, but this is not true for $\mathbf C - \boldsymbol \Psi$.

So yes, @gung and @ttnphns are right in that FA is based on a generative model and PCA is not, but I think it is important to add that PPCA is also based on a generative model, but is "almost" equivalent to PCA. Then it ceases to seem such an important difference.

---

Update 2: how come PCA provides best approximation to the covariance matrix, when it is well-known to be looking for maximal variance?

PCA has two equivalent formulations: e.g. first PC is (a) the one maximizing the variance of the projection and (b) the one providing minimal reconstruction error. More abstractly, the equivalence between maximizing variance and minimizing reconstruction error can be seen using Eckart-Young theorem.

If $\mathbf X$ is the data matrix (with observations as rows, variables as columns, and columns are assumed to be centered) and its SVD decomposition is $\mathbf X=\mathbf U\mathbf S\mathbf V^\top$, then it is well known that columns of $\mathbf V$ are eigenvectors of the scatter matrix (or covariance matrix, if divided by the number of observations) $\mathbf C=\mathbf X^\top \mathbf X=\mathbf V\mathbf S^2\mathbf V^\top$ and so they are axes maximizing the variance (i.e. principal axes). But by the Eckart-Young theorem, first $k$ PCs provide the best rank-$k$ approximation to $\mathbf X$: $\mathbf X_k=\mathbf U_k\mathbf S_k \mathbf V^\top_k$ (this notation means taking only $k$ largest singular values/vectors) minimizes $\|\mathbf X-\mathbf X_k\|^2$.

The first $k$ PCs provide not only the best rank-$k$ approximation to $\mathbf X$, but also to the covariance matrix $\mathbf C$. Indeed, $\mathbf C=\mathbf X^\top \mathbf X=\mathbf V\mathbf S^2\mathbf V^\top$, and the last equation provides the SVD decomposition of $\mathbf C$ (because $\mathbf V$ is orthogonal and $\mathbf S^2$ is diagonal). So the Eckert-Young theorem tells us that the best rank-$k$ approximation to $\mathbf C$ is given by $\mathbf C_k = \mathbf V_k\mathbf S_k^2\mathbf V_k^\top$. This can be transformed by noticing that $\mathbf W = \mathbf V\mathbf S$ are PCA loadings, and so $$\mathbf C_k=\mathbf V_k\mathbf S_k^2\mathbf V^\top_k=(\mathbf V\mathbf S)_k(\mathbf V\mathbf S)_k^\top=\mathbf W_k\mathbf W^\top_k.$$

The bottom-line here is that $$ \mathrm{minimizing} \; \left\{\begin{array}{ll} \|\mathbf C-\mathbf W\mathbf W^\top\|^2 \\ \|\mathbf C-\mathbf W\mathbf W^\top-\sigma^2\mathbf I\|^2 \\ \|\mathbf C-\mathbf W\mathbf W^\top-\boldsymbol\Psi\|^2\end{array}\right\} \; \mathrm{leads \: to} \; \left\{\begin{array}{cc} \mathrm{PCA}\\ \mathrm{PPCA} \\ \mathrm{FA} \end{array}\right\} \; \mathrm{loadings},$$ as stated in the beginning.

---

Update 3: numerical demonstration that PCA$\to$FA when $n \to \infty$

I was encouraged by @ttnphns to provide a numerical demonstration of my claim that as dimensionality grows, PCA solution approaches FA solution. Here it goes.

I generated a $200\times 200$ random correlation matrix with some strong off-diagonal correlations. I then took the upper-left $n \times n$ square block $\mathbf C$ of this matrix with $n=25, 50, \dots 200$ variables to investigate the effect of the dimensionality. For each $n$, I performed PCA and FA with number of components/factors $k=1\dots 5$, and for each $k$ I computed the off-diagonal reconstruction error $$\sum_{i\ne j}\left[\mathbf C - \mathbf W \mathbf W^\top\right]^2_{ij}$$ (note that on the diagonal, FA reconstructs $\mathbf C$ perfectly, due to the $\boldsymbol \Psi$ term, whereas PCA does not; but the diagonal is ignored here). Then for each $n$ and $k$, I computed the ratio of the PCA off-diagonal error to the FA off-diagonal error. This ratio has to be above $1$, because FA provides the best possible reconstruction.

On the right, different lines correspond to different values of $k$, and $n$ is shown on the horizontal axis. Note that as $n$ grows, ratios (for all $k$) approach $1$, meaning that PCA and FA yield approximately the same loadings, PCA$\approx$FA. With relatively small $n$, e.g. when $n=25$, PCA performs [expectedly] worse, but the difference is not that strong for small $k$, and even for $k=5$ the ratio is below $1.2$.

The ratio can become large when the number of factors $k$ becomes comparable with the number of variables $n$. In the example I gave above with $n=2$ and $k=1$, FA achieves $0$ reconstruction error, whereas PCA does not, i.e. the ratio would be infinite. But getting back to the original question, when $n=21$ and $k=3$, PCA will only moderately lose to FA in explaining the off-diagonal part of $\mathbf C$.

For an illustrated example of PCA and FA applied to a real dataset (wine dataset with $n=13$), see my answers here:

• What are the differences between Factor Analysis and Principal Component Analysis?
• PCA and exploratory Factor Analysis on the same data set

Answer 2

As you said, you are familiar with relevant answers; see also: So, as long as "Factor analysis..." + a couple of last paragraphs; and the bottom list here. In short, PCA is mostly a data reduction technique whereas FA is a modeling-of-latent-traits technique. Sometimes they happen to give similar results; but in your case - because you probably feel like constructing/validating latent traits as if real entities - using FA would be more honest and you shouldn't prefer PCA in hope that their results converge. On the other hand, whenever you aim to summarise/simplify the data - for subsequent analysis, for example - you would prefer PCA, as it doesn't impose any strong model (which might be irrelevant) on the data.

To reiterate other way, PCA gives you dimensions which may correspond to some subjectively meaningful constructs, if you wish, while EFA poses that those are even covert features that actually generated your data, and it aims to find those features. In FA, interpretation of the dimensions (factors) is pending - whether you can attach a meaning to a latent variable or not, it "exists" (FA is essentialistic), otherwise you should drop it from the model or get more data to support it. In PCA, the meaning of a dimension is optional.

And yet once again in other words: When you extract m factors (separate factors from errors), these few factors explain (almost) all correlation among variables, so that the variables are not left room to correlate via the errors anyhow. Therefore, so long as "factors" are defined as latent traits which generate/bind the correlated data, you have full clues to interpret that - what is responsible for the correlations. In PCA (extract components as if "factors"), errors (may) still correlate between the variables; so you can't claim that you've extracted something enough clean and exhaustive to be interpreted in that way.

You may want to read my other, longer answer in the current discussion, for some theoretical and simulation experiment details about whether PCA is a viable substitute of FA. Please pay attention also to outstanding answers by @amoeba given on this thread.

---

Upd: In their answer to this question @amoeba, who opposed there, introduced a (not well-known) technique PPCA as standing halfway between PCA and FA. This naturally launched the logic that PCA and FA are along one line rather than opposite. That valuable approach expands one's theoretical horizons. But it can mask the important practical difference about that FA reconstructs (explains) all the pairwise covariances with a few factors, while PCA cannot do it successfully (and when it occasionally does it - that is because it happened to mime FA).

Answer 3

Part 1. Pictures & theory

---

In this my answer (a second and additional to the other of mine here) I will try to show in pictures that PCA does not restore a covariance any well (whereas it restores - maximizes - variance optimally).

As in a number of my answers on PCA or Factor analysis I will turn to vector representation of variables in subject space. In this instance it is but a loading plot showing variables and their component loadings. So we got $X_1$ and $X_2$ the variables (we had only two in the dataset), $F$ their 1st principal component, with loadings $a_1$ and $a_2$. The angle between the variables is also marked. Variables were centered preliminary, so their squared lengths, $h_1^2$ and $h_2^2$ are their respective variances.

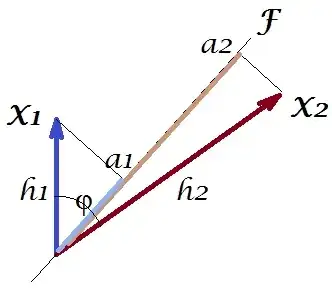
The covariance between $X_1$ and $X_2$ is - it is their scalar product - $h_1 h_2 cos \phi$ (this cosine is the correlation value, by the way). Loadings of PCA, of course, capture the maximum possible of the overall variance $h_1^2+h_2^2$ by $a_1^2+a_2^2$, the component $F$'s variance.

Now, the covariance $h_1 h_2 cos \phi = g_1 h_2$, where $g_1$ is the projection of variable $X_1$ on variable $X_2$ (the projection which is the regression prediction of the first by the second). And so the magnitude of the covariance could be rendered by the area of the rectangle below (with sides $g_1$ and $h_2$).

According to the so called "factor theorem" (might know if you read something on factor analysis), covariance(s) between variables should be (closely, if not exactly) reproduced by multiplication of loadings of the extracted latent variable(s) (read). That is, by, $a_1 a_2$, in our particular case (if to recognize the principal component to be our latent variable). That value of the reproduced covariance could be rendered by the area of a rectangle with sides $a_1$ and $a_2$. Let us draw the rectangle, aligned by the previous rectangle, to compare. That rectangle is shown hatched below, and its area is nicknamed cov* (reproduced cov).

It's obvious that the two areas are pretty dissimilar, with cov* being considerably larger in our example. Covariance got overestimated by the loadings of $F$, the 1st principal component. This is contrary to somebody who might expect that PCA, by the 1st component alone of the two possible, will restore the observed value of the covariance.

What could we do with our plot to enchance the reproduction? We can, for example, rotate the $F$ beam clockwise a bit, even until it superposes with $X_2$. When their lines coincide, that means that we forced $X_2$ to be our latent variable. Then loading $a_2$ (projection of $X_2$ on it) will be $h_2$, and loading $a_1$ (projection of $X_1$ on it) will be $g_1$. Then two rectangles are the same one - the one that was labeled cov, and so the covariance is reproduced perfectly. However, $g_1^2 + h_2^2$, the variance explained by the new "latent variable", is smaller than $a_1^2 + a_2^2$, the variance explained by the old latent variable, the 1st principal component (square and stack the sides of each of the two rectangles on the picture, to compare). It appears that we managed to reproduce the covariance, but at expense of explaining the amount of variance. I.e. by selecting another latent axis instead of the first principal component.

Our imagination or guess may suggest (I won't and possibly cannot prove it by math, I'm not a mathematician) that if we release the latent axis from the space defined by $X_1$ and $X_2$, the plane, allowing it to swing a bit towards us, we can find some optimal position of it - call it, say, $F^*$ - whereby the covariance is again reproduced perfectly by the emergent loadings ($a_1^* a_2^*$) while the variance explained ($a_1^{*2} + a_2^{*2}$) will be bigger than $g_1^2 + h_2^2$, albeit not as big as $a_1^2 + a_2^2$ of the principal component $F$.

I believe that this condition is achievable, particularly in that case when the latent axis $F^*$ gets drawn extending out of the plane in such a way as to pull a "hood" of two derived orthogonal planes, one containing the axis and $X_1$ and the other containing the axis and $X_2$. Then this latent axis we'll call the common factor, and our entire "attempt at originality" will be named factor analysis.

---

Part 2. A reply to @amoeba's "Update 2" in respect to PCA.

@amoeba is correct and relevant to recall Eckart-Young theorem which is fundamental to PCA and its congeneric techniques (PCoA, biplot, correspondence analysis) based on SVD or eigen-decomposition. According to it, $k$ first principal axes of $\bf X$ optimally minimize $\bf ||X-X_k||^2$ - a quantity equal to $\bf tr(X'X)-tr(X_k'X_k)$, - as well as $\bf ||X'X-X_k'X_k||^2$. Here $\bf X_k$ stands for the data as reproduced by the $k$ principal axes. $\bf X_k'X_k$ is known to be equal to $\bf W_k W_k'$, with $\bf W_k$ being the variable loadings of the $k$ components.

Does it mean that minimization $\bf ||X'X-X_k'X_k||^2$ remain true if we consider only off-diagonal portions of both symmetric matrices? Let's inspect it by experimenting.

500 random 10x6 matrices $\bf X$ were generated (uniform distribution). For each, after centering its columns, PCA was performed, and two reconstructed data matrices $\bf X_k$ computed: one as reconstructed by components 1 through 3 ($k$ first, as usual in PCA), and the other as reconstructed by components 1, 2, and 4 (that is, component 3 was replaced by a weaker component 4). The reconstruction error $\bf ||X'X-X_k'X_k||^2$ (sum of squared difference = squared Euclidean distance) was then computed for one $\bf X_k$, for the other $\bf X_k$. These two values is a pair to show on a scatterplot.

The reconstruction error was computed each time in two versions: (a) whole matrices $\bf X'X$ and $\bf X_k'X_k$ compared; (b) only off-diagonals of the two matrices compared. Thus, we have two scatterplots, with 500 points each.

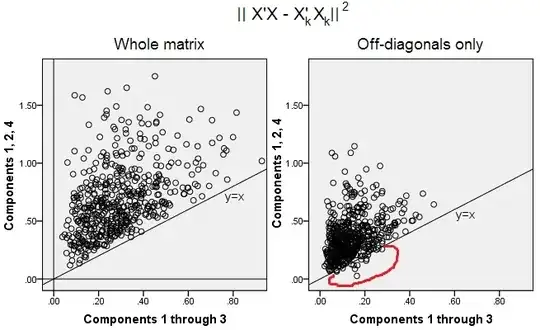
We see, that on the "whole matrix" plot all points lie above y=x line. Which means that the reconstruction for the whole scalar-product matrix is always more accurate by "1 through 3 components" than by "1, 2, 4 components". This is in line with Eckart-Young theorem says: first $k$ principal components are the best fitters.

However, when we look at "off-diagonals only" plot we notice a number of points below the y=x line. It appeared that sometimes reconstruction of off-diagonal portions by "1 through 3 components" was worse than by "1, 2, 4 components". Which automatically leads to the conclusion that first $k$ principal components are not regularly the best fitters of off-diagonal scalar products among fitters available in PCA. For example, taking a weaker component instead of a stronger may sometimes improve the reconstruction.

So, even in the domain of PCA itself, senior principal components - who do approximate overall variance, as we know, and even the whole covariance matrix, too, - not necessarily approximate off-diagonal covariances. Better optimization of those is required therefore; and we know that factor analysis is the (or among the) technique that can offer it.

---

Part 3. A follow-up to @amoeba's "Update 3": Does PCA approach FA as the number of variables grows? Is PCA a valid substitute of FA?

I've conducted a lattice of simulation studies. A few number of population factor structures, loading matrices $\bf A$ were constructed of random numbers and converted to their corresponding population covariance matrices as $\bf R=AA'+ U^2$, with $\bf U^2$ being a diagonal noise (unique variances). These covariance matrices were made with all variances 1, therefore they were equal to their correlation matrices.

Two types of factor structure were designed - sharp and diffuse. Sharp structure is one having clear simple structure: loadings are either "high" of "low", no intermediate; and (in my design) each variable is highly loaded exactly by one factor. Corresponding $\bf R$ is hence noticebly block-like. Diffuse structure does not differentiate between high and low loadings: they can be any random value within a bound; and no pattern within loadings is conceived. Consequently, corresponding $\bf R$ comes smoother. Examples of the population matrices:

The number of factors was either $2$ or $6$. The number of variables was determined by the ratio k = number of variables per factor; k ran values $4,7,10,13,16$ in the study.

For each of the few constructed population $\bf R$, $50$ its random realizations from Wishart distribution (under sample size n=200) were generated. These were sample covariance matrices. Each was factor-analyzed by FA (by principal axis extraction) as well as by PCA. Additionally, each such covariance matrix was converted into corresponding sample correlation matrix that was also factor-analyzed (factored) same ways. Lastly, I also performed factoring of the "parent", population covariance (=correlation) matrix itself. Kaiser-Meyer-Olkin measure of sampling adequacy was always above 0.7.

For data with 2 factors, the analyses extracted 2, and also 1 as well as 3 factors ("underestimation" and "overestimation" of the correct number of factors regimes). For data with 6 factors, the analyses likewise extracted 6, and also 4 as well as 8 factors.

The aim of the study was the covariances/correlations restoration qualities of FA vs PCA. Therefore residuals of off-diagonal elements were obtained. I registered residuals between the reproduced elements and the population matrix elements, as well as residuals between the former and the analyzed sample matrix elements. The residuals of the 1st type were conceptually more interesting.

Results obtained after analyses done on sample covariance and on sample correlation matrices had certain differences, but all the principal findings occured to be similar. Therefore I'm discussing (showing results) only of the "correlations-mode" analyses.

1. Overall off-diagonal fit by PCA vs FA

The graphics below plot, against various number of factors and different k, the ratio of the mean squared off-diagonal residual yielded in PCA to the same quantity yielded in FA. This is similar to what @amoeba showed in "Update 3". The lines on the plot represent average tendencies across the 50 simulations (I omit showing st. error bars on them).

(Note: the results are about factoring of random sample correlation matrices, not about factoring the population matrix parental to them: it is silly to compare PCA with FA as to how well they explain a population matrix - FA will always win, and if the correct number of factors is extracted, its residuals will be almost zero, and so the ratio would rush towards infinity.)

Commenting these plots:

• General tendency: as k (number of variables per factor) grows the PCA/FA overall subfit ratio fades towards 1. That is, with more variables PCA approaches FA in explaining off-diagonal correlations/covariances. (Documented by @amoeba in his answer.) Presumably the law approximating the curves is ratio= exp(b0 + b1/k) with b0 close to 0.
• Ratio is greater w.r.t. residuals “sample minus reproduced sample” (left plot) than w.r.t. residuals “population minus reproduced sample” (right plot). That is (trivially), PCA is inferior to FA in fitting the matrix being immediately analyzed. However, lines on the left plot have faster rate of decrease, so by k=16 the ratio is below 2, too, as it is on the right plot.
• With residuals “population minus reproduced sample”, trends are not always convex or even monotonic (the unusual elbows are shown circled). So, as long as speech is about explaining a population matrix of coefficients via factoring a sample, rising the number of variables does not regularly bring PCA closer to FA in its fittinq quality, though the tendency is there.
• Ratio is greater for m=2 factors than for m=6 factors in population (bold red lines are below bold green lines). Which means that with more factors acting in the data PCA sooner catches up with FA. For example, on the right plot k=4 yields ratio about 1.7 for 6 factors, while the same value for 2 factors is reached at k=7.
• Ratio is higher if we extract more factors relative the true number of factors. That is, PCA is only slightly worse a fitter than FA if at extraction we underestimate the number of factors; and it loses more to it if the number of factors is correct or overestimated (compare thin lines with bold lines).
• There is an interesting effect of the sharpness of factor structure which appears only if we consider residuals “population minus reproduced sample”: compare grey and yellow plots on the right. If population factors load variables diffusely, red lines (m=6 factors) sink to the bottom. That is, in diffuse structure (such as loadings of chaotic numbers) PCA (performed on a sample) is only few worse than FA in reconstructing the population correlations- even under small k, provided that the number of factors in the population isn’t very small. This is probably the condition when PCA is most close to FA and is most warranted as its cheeper substitute. Whereas in the presence of sharp factor structure PCA isn’t so optimistic in reconstructing the population correlations (or covariances): it approaches FA only in big k perspective.

2. Element-level fit by PCA vs FA: distribution of residuals

For every simulation experiment where factoring (by PCA or FA) of 50 random sample matrices from the population matrix was performed, distribution of residuals "population correlation minus reproduced (by the factoring) sample's correlation" was obtained for every off-diagonal correlation element. Distributions followed clear patterns, and examples of typical distributions are depicted right below. Results after PCA factoring are blue left sides and results after FA factoring are green right sides.

The principal finding is that

• Pronounced, by absolute magnitude, population correlations are restored by PCA inadequetly: the reproduced values are overestimates by magnitude.
• But the bias vanishes as k (number of variables to number of factors ratio) increases. On the pic, when there is only k=4 variables per factor, PCA's residuals spread in offset from 0. This is seen both when there exist 2 factors and 6 factors. But with k=16 the offset is hardly seen - it almost dissapeared and PCA fit approaches FA fit. No difference in spread (variance) of residuals between PCA and FA is observed.

Similar picture is seen also when the number of factors extracted does not match true number of factors: only variance of residuals somewhat change.

The distributions shown above on grey background pertain to the experiments with sharp (simple) factor structure present in the population. When all the analyses were done in situation of diffuse population factor structure, it was found that the bias of PCA fades away not only with the rise of k, but also with the rise of m (number of factors). Please see the scaled down yellow-background attachments to the column "6 factors, k=4": there is almost no offset from 0 observed for PCA results (the offset is yet present with m=2, that is not shown on the pic).

Thinking that the described findings are important I decided to inspect those residual distributions deeper and plotted the scatterplots of the residuals (Y axis) against the element (population correlation) value (X axis). These scatterplots each combine results of all the many (50) simulations/analyses. LOESS fit line (50% local points to use, Epanechnikov kernel) is highlighted. The first set of plots is for the case of sharp factor structure in the population (the trimodality of correlation values is apparent therefore):

Commenting:

• We clearly see the (described above) reconstuction bias which is characteristic of PCA as the skew, negative trend loess line: big in absolute value population correlations are overestimated by PCA of sample datasets. FA is unbiased (horizontal loess).
• As k grows, PCA's bias diminishes.
• PCA is biased irrespective of how many factors there are in the population: with 6 factors existent (and 6 extracted at analyses) it is similarly defective as with 2 factors existent (2 extracted).

The second set of plots below is for the case of diffuse factor structure in the population:

Again we observe the bias by PCA. However, as opposed to sharp factor structure case, the bias fades as the number of factors increases: with 6 population factors, PCA's loess line is not very far from being horizontal even under k only 4. This is what we've expressed by "yellow histograms" earlier.

One interesting phenomenon on both sets of scatterplots is that loess lines for PCA are S-curved. This curvature shows under other population factor structures (loadings) randomly constructed by me (I checked), although its degree varies and is often weak. If follows from the S-shape then that PCA starts to distort correlations rapidly as they bounce from 0 (especially under small k), but from some value on - around .30 or .40 - it stabilizes. I will not speculate at this time for possible reason of that behavior, althougt I believe the "sinusoid" stems from the triginometric nature of correlation.

3. Fit by PCA vs FA: Conclusions

As the overall fitter of the off-diagonal portion of a correlation/covariance matrix, PCA - when applied to analyze a sample matrix from a population - can be a fairly good substitute for factor analysis. This happens when the ratio number of variables / number of expected factors is big enough. (Geometrical reason for the beneficial effect of the ratio is explained in the bottom Footnote $^1$.) With more factors existent the ratio may be less than with only few factors. The presence of sharp factor structure (simple structure exists in the population) hampers PCA to approach the quality of FA.

The effect of sharp factor structure on the overall fit ability of PCA is apparent only as long as residuals "population minus reproduced sample" are considered. Therefore one can miss to recognize it outside a simulation study setting - in an observational study of a sample we don't have access to these important residuals.

Unlike factor analysis, PCA is a (positively) biased estimator of the magnitude of population correlations (or covariances) that are away from zero. The biasedness of PCA however decreases as the ratio number of variables / number of expected factors grows. The biasedness also decreases as the number of factors in the population grows, but this latter tendency is hampered under a sharp factor structure present.

I would remark that PCA fit bias and the effect of sharp structure on it can be uncovered also in considering residuals "sample minus reproduced sample"; I simply omitted showing such results because they seem not to add new impressions.

My very tentative, broad advice in the end might be to refrain from using PCA instead of FA for typical (i.e. with 10 or less factors expected in the population) factor analytic purposes unless you have some 10+ times more variables than the factors. And the fewer are factors the severer is the necessary ratio. I would further not recommend using PCA in place of FA at all whenever data with well-established, sharp factor structure is analyzed - such as when factor analysis is done to validate the being developed or already launched psychological test or questionnaire with articulated constructs/scales . PCA may be used as a tool of initial, preliminary selection of items for a psychometric instrument.

Limitations of the study. 1) I used only PAF method of factor extraction. 2) The sample size was fixed (200). 3) Normal population was assumed in sampling the sample matrices. 4) For sharp structure, there was modeled equal number of variables per factor. 5) Constructing population factor loadings I borrowed them from roughly uniform (for sharp structure - trimodal, i.e. 3-piece uniform) distribution. 6) There could be oversights in this instant examination, of course, as anywhere.

---

Footnote $1$. PCA will mimic results of FA and become the equivalent fitter of the correlations when - as said here - error variables of the model, called unique factors, become uncorrelated. FA seeks to make them uncorrelated, but PCA doesn't, they may happen to be uncorrelated in PCA. The major condition when it may occur is when the number of variables per number of common factors (components kept as common factors) is large.

Consider the following pics (if you need first to learn how to understand them, please read this answer):

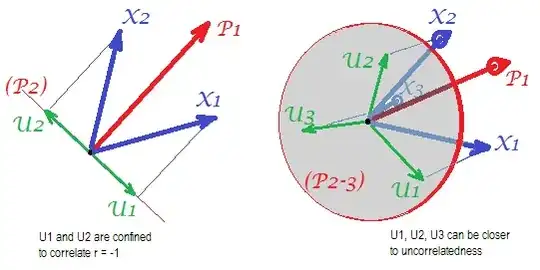
By the requirement of factor analysis to be able to restore succesfully correlations with few m common factors, unique factors $U$, characterizing statistically unique portions of the p manifest variables $X$, must be uncorrelated. When PCA is used, the p $U$s have to lie in the p-m subspace of the p-space spanned by the $X$s because PCA does not leave the space of the analyzed variables. Thus - see the left pic - with m=1 (principal component $P_1$ is the extracted factor) and p=2 ($X_1$, $X_2$) analyzed, unique factors $U_1$, $U_2$ compulsorily superimpose on the remaining second component (serving as error of the analysis). Consequently they have to be correlated with $r=-1$. (On the pic, correlations equal cosines of angles between vectors.) The required orthogonality is impossible, and the observed correlation between the variables can never be restored (unless the unique factors are zero vectors, a trivial case).

But if you add one more variable ($X_3$), right pic, and extract still one pr. component as the common factor, the three $U$s have to lie in a plane (defined by the remaining two pr. components). Three arrows can span a plane in a way that angles between them are smaller than 180 degrees. There freedom for the angles emerges. As a possible particular case, the angles can be about equal, 120 degrees. That is already not very far from 90 degrees, that is, from uncorrelatedness. This is the situation shown on the pic.

As we add 4th variable, 4 $U$s will be spanning 3d space. With 5, 5 to span 4d, etc. Room for a lot of the angles simultaneously to attain closer to 90 degrees will expand. Which means that the room for PCA to approach FA in its ability to fit off-diagonal triangles of correlation matrix will also expand.

But true FA is usually able to restore the correlations even under small ratio "number of variables / number of factors" because, as explained here (and see 2nd pic there) factor analysis allows all the factor vectors (common factor(s) and unique ones) to deviate from lying in the variables' space. Hence there is the room for the orthogonality of $U$s even with only 2 variables $X$ and one factor.

The more diffuse (the less sharp) is the factor structure - that is, the more unimodal or even is the distribution of the factor loadings, - the closer the above said orthogonality is to become real, realized; the better is PCA executing the role of FA.

The pics above also give obvious clue to why PCA overestimates correlations. On the left pic, for example, $r_{X_1X_2}= a_1a_2 - u_1u_2$, where the $a$s are the projections of the $X$s on $P_1$ (loadings of $P_1$) and the $u$s are the lengths of the $U$s (loadings of $P_2$). But that correlation as reconstructed by $P_1$ alone equals just $a_1a_2$, i.e. bigger than $r_{X_1X_2}$.

Answer 4

(This is really a comment to @ttnphns's second answer)
As far as the different type of reproduction of covariance assuming error by PC and by FA is concerned, I've simply printed out the loadings/components of variance which occur in the two procedures; just for the examples I took 2 variables.

We assume the construction of the two items as of one common factor and itemspecific factors. Here is that factor-loadingsmatrix:

  L_fa: 
          f1       f2      f3         
  X1:   0.894    0.447     .             
  X1:   0.894     .       0.447              

The correlation matrix by this is

  C:
         X1       X2 
  X1:   1.000   0.800
  X2:   0.800   1.000

If we look at the loadings-matrix L_fa and interpret it as usual in FA that f2 and f3 are error terms/itemspecific error, we reproduce C without that error, receiving

 C1_Fa 
        X1       X2 
 X1:  0.800   0.800
 X2:  0.800   0.800

So we have perfectly reproduced the off-diagonal element, which is the covariance (and the diagonal is reduced)

If we look at the pca-solution (can be done by simple rotations) we get the two factors from the same correlation-matrix:

 L_pca : 
         f1        f2
 X1:   0.949      -0.316
 X2:   0.949       0.316

Assuming the second factor as error we get the reproduced matrix of covariances

  C1_PC : 
        X1      X2
 X1:   0.900   0.900
 X2:   0.900   0.900

where we've overestimated the true correlation. This is because we ignored the correcting negative partial covariance in the second factor = error. Note that the PPCA would be identical with the first example.

With more items this is no more so obvious but still an inherent effect. Therefore there is also the concept of MinRes-extraction (or -rotation?) and I've also seen something like maximum-determinant extraction and...

---

[update] As for the question of @amoeba:

I understood the concept of "Minimal Residuals" ("MinRes")-rotation as a concurring method to the earlier methods of CFA-computation, to achieve the best reproduction of the off-diagonal elements of a correlation matrix. I learned this in the 80'ies/90'ies and didn't follow the development of factor-analysis (as indepth as before in the recent years), so possibly "MinRes" is out of fashion.

To compare it with the PCA-solution: one can think of finding the pc-solution by rotations of the factors when they are thought as axes in an euclidean space and the loadings are the coordinates of the items in that vectorspace.
Then for a pair of axes say x,y the sums-of-squares from the loadings of the x-axis and that of the y-axis are computed.
From this one can find a rotation angle, by which we should rotate, to get the sums-of-squares in the rotated axes maximal on the x° and minimal on the y°-axis (where the little circle indicates the rotated axes).

Doing this for all pairs of axes (where only always the x-axis is the left and the y-axis is the right (so for 4 factors we have only 6 pairs of rotation)) and then repeat the whole process to a stable result realizes the so-called "Jacobi-method" for the finding of the principal components solution: it will locate the first axis such that it collects the maximum possible sum of squares of loadings ("SSqL") (which means also "of the variance") on one axis in the current correlational configuration.

As far as I understood things, "MinRes" should look at the partial correlations instead of the SSqL; so it does not sum up the squares of the loadings (as done in the Jacobi-pc-rotation) but is sums up the crossproducts of the loadings in each factor - except of the "crossproducts" (=squares) of the loadings of each item with itself.
After the criteria for the x and for the y-axis are computed it proceeds the same way as described for the iterative Jacobi-rotation.

Since the rotation-criterion is numerically different from the maximum-SSqL-criterion the result/the rotational position shall be different from the PCA-solution. If it converges it should instead provide the maximum possible partial correlation on one axis in the first factor, the next maximal correlation on the next factor and so on. The idea seems to be, then to assume so many axes/factors such that the remaining/residual partial covariance becomes marginal.

(Note this is only how I interpreted things, I've not seen that procedure explicitly written out (or cannot remember at the moment); a description at mathworld seems to express it rather in terms of the formulae like in amoeba's answer) and is likely more authoritative. Just found another reference in the R-project documentation and a likely very good reference in the Gorsuch book on factoranalysis, page 116, available via google-books)

Answer 5

In my view, the notions of "PCA" and "FA" are on a different dimension from that of notions of "exploratory", "confirmatory" or maybe "inferential". So each of the two mathematical/statistical methods can be applied with one of the three approaches.

For instance, why should it be unsensical to have a hypothese, that my data have a general factor and also the structure of a set of principal components (because my experiment with my electronical apparatus gave me nearly errorfree data) and I test my hypothese, that the eigenvalues of the subsequent factors occur with ratio of 75% ? This is then PCA in a confirmatory framework.

On the other hand, it seems ridiculous that in our research team we create with much work an item battery for measuring violence between pupils and assuming 3 main behaves (physical agression, depression, search for help by authorities/parents) and putting the concerning questions in that battery ... and "exploratorily" work out how many factors we have... Instead to look, how well our scale contains three recognizable factors (besides neglectable itemspecific and possibly even spuriously correlated error). And after that, when I've confirmed, that indeed our item-battery serves the intention, we might test the hypothese, that in the classes of younger children the loadings on the factor indicating "searching-help-by-authorities" are higher than that of older pupils. Hmmm, again confirmatory...

And exploratory? I have a set of measures taken from a research on microbiology from 1960 and they had not much theory but sampled everything they could manage because their field of research was just very young, and I re-explore the dominant factorstructure, assuming (for example), that all errors are of the same amount because of the optical precision of the microscope used (the ppca-ansatz as I have just learnt). Then I use the statistical (and subsequently the mathematical) model for the FA, but in this case in an explorative manner.

This is it at least how I understand the terms.
Maybe I'm completely on the wrong track here, but I don't assume it.

---

Ps. In the 90'ies I wrote a small interactive program to explore the method of PCA and factoranalysis down to the bottom. It was written in Turbo-Pascal, can still only be run in a Dos-Window ("Dos-box" under Win7) but has a really nice appeal: interactively switching factors to be included or not, then rotate, separate itemspecific error-variance (according to the SMC-criterion or the equal-variances-criterion (ppca?)), switch the Kaiser-option on and off, the use of the covariances on and off - just all while the factorloadingsmatrix is visible like in a spreadsheet and can be rotated for the basic different rotation-methods.
It is not highly sophisticated: no chisquare-test for instance, just intended for self-learning of the internal mathematical mechanics. It has also a "demo-mode", where the program runs itself, showing explanative comments on the screen and simulating the keyboard-inputs, which the user normally would do.
Whoever is interested to do selfstudy or teaching with it can download it from my small software-pages inside-(R).zip Just expand the files in the zip in a directory accessible by the Dos-Box and call "demoall.bat" In the third part of the "demoall" I've made a demonstration how to model itemspecific errors by rotations from an initially pca-solution...

Answer 6

Just one additional remark for @amoebas's long (and really great) answer on the character of the $\Psi$-estimate.

In your initial statements you have three $\Psi$: for PCA is $ \Psi = 0$, for PPCA is $ \Psi=\sigma ^2 I $ and for FA you left $\Psi$ indeterminate.

But it should be mentioned, that there is an infinite number of various possible $\Psi$ (surely restricted) but exactly a single one which minimizes the rank of the factor matrix. Let's call this $\Psi_{opt}$ The standard (automatical) estimate for $\Psi_{std}$ is the diagonalmatrix based on the SMC's, so let's write this as $\Psi_{std}= \alpha^2 D_{smc}$ (and even some software (seem to) do not attempt to optimize $\alpha$ down from $1$ while $ \alpha \lt 1$ is (generally) required to prevent Heywood-cases/negative-definiteness). And moreover, even such optimized $\alpha^2$ would not guarantee minimal rank of the remaining covariances, thus usually we have this not equal: in general $\Psi_{std} \ne \Psi_{opt}$.
To really find $\Psi_{opt}$ is a very difficult game, and as far as I know (but that's no more so "far" as, say, 20 years ago when I was more involved and nearer to the books) this is still an unsolved problem.

---

Well this reflects the ideal, mathematical side of the problem, and my distinction between $\Psi_{std} $ and $\Psi_{opt}$ also might be actually small. A more general caveat is however, that it discusses the whole factorization machinery from the view that I study only my sample or have data of the whole population; in the model of inferential statistics, where I infer from an imperfect sample on the population, my empirical covariance- and thus also the factormatrix is only an estimate, it's only a shadow of the "true" covariance-/factormatrix. Thus in such a framework/model we should even consider that our "errors" are not ideal, and thus might be spuriously correlated. So in fact in such models we should/would leave the somehow idealistic assumption of uncorrelated error, and thus of a strictly diagonal form of $\Psi$, behind us.