3

Let's assume for the sake of argument that I am not out to TPK my players when we sit down to play a narrative game based on martial arts movies. That said, it would be nice to be able to engage in fine-grained reasoning about exactly how tough I can make a boss battle before it starts to look grim for our heroes.

A Nemesis arrives on the scene with X Chi. Players do some number of hits each round, and he responds in kind. Players do win ties, as the rules state:

If a hero and a Nemesis score hits on each other in the same round, hits that neither of them can block with Yin or Chi, then whoever takes the most hits loses. If they tie, victory goes to the player.

This suggests to me - absent the tiebreaking rule, and ignoring the fact that both players and Director may roll Yin to block any number of hits per round - that a Nemesis would be considered an even match at X Chi, where X is the sum of all players' Chi at the start of the battle (max 3 * player count). Of course, to the exhaustive GM, this leaves only one question unanswered.

Given that players win ties for victory, how much Chi does a Nemesis need to be considered an even match, and how quickly does its deadliness increase beyond that level?

Please do not feel the need to point out that a Nemesis fight of this level is almost certainly never called-for in-game; this is an academic inquiry.

Matthieu
  • 9,017
  • 2
  • 18
  • 66
order
  • 3,865
  • 2
  • 15
  • 51

1 Answers1

1

The breakeven point (50% chance of Nemesis win) is around (player Chi) + 10-50% (increasing with the difference in player and Nemesis combat skill).

(see also: posita's answer to my other related question, which corroborates this analysis with a superior model.

For larger pools, the percentage value is smaller, but still positive.

Jasper Flick, creator of Anydice, helped me write a program that iterates over a constant number of rounds, instead of using computationally expensive recursion to cover all possible round outcomes. You can just email him! The "Support Chat" button really works!

In the analysis below:

  • 0 represents both players and Nemesis are still standing
  • 1 indicates players won without losing all Chi,
  • 2 indicates Nemesis won,
  • 3 represents a tie where both parties died (and players won, per rules).
  • All parties throw only Yang hits.

A graph is worth a thousand words. Below, find the cumulative percentage graphs of Chi values 1-20 over the first 5 rounds of combat:

Player Skill 5 vs. Nemesis Skill 5

Nemesis Chi = Player Chi

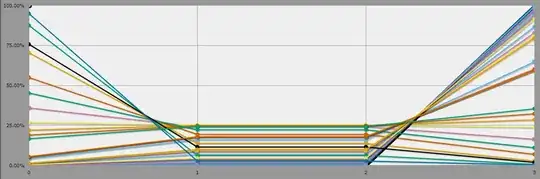
Graph of player vs nemesis chi showing that the max limit seems to be 25% win in 5 rounds

For equally matched skills and Chi pools, the maximum limit seems to be 25% for a Nemesis win, even 5 rounds in at 20 Chi.

I tested up to 10 rounds with 40 Chi and the 25% limit held - in fact, it seemed to shrink lower again as Chi increased.

Nemesis Chi = Player Chi + 10%

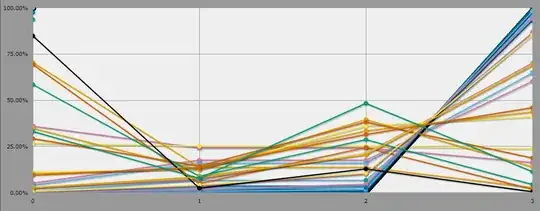
Graph of player vs nemesis chi showing that the odds of Nemesis win increase as total Chi increases up to 50% at 20 vs 22 Chi

For equally matched skill pools where the Nemesis has 10% more Chi than the total player pool, the odds of Nemesis victory increase as player Chi increases, up to about 50% for a firecracker of a 20-Chi brawl where the Nemesis has 22.

Nemesis Chi = Player Chi + 50%

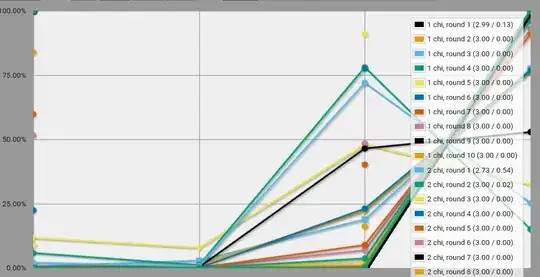
graph illustrating nemesis spike at mid-10 chi

This is a nice, varied graph. For example, at 6 vs 9 Chi, Nemeses have a 78% chance(!) of winning round 2, but an abysmal 3% thereafter. This "early spike" seems to manifest later in the combat as Chi pools grow, and it climbs higher.

When combat skills are equal, a Chi differential of 50% is immense.

Player skill 5 vs. Nemesis skill 4

Nemesis Chi = Player Chi

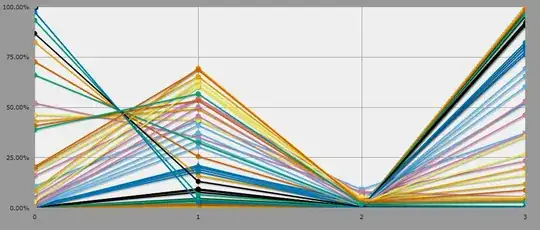
Graph indicating Nemeses don't stand a chance

Odds of a Nemesis victory fall to 0 as Chi rises, as expected.

Nemesis Chi = Player Chi + 10%

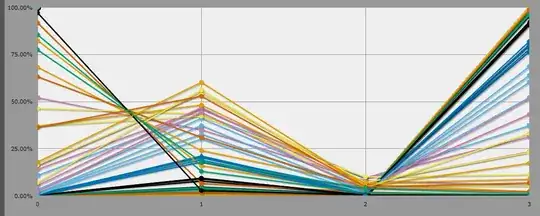
Graph indicating Nemeses still don't stand a chance

Odds of the bad guys winning do not improve much with the addition of 10% extra Chi.

Nemesis Chi = Player Chi + 50%

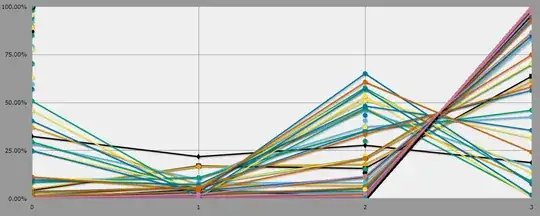
Graph indicating Nemeses start to have >50% kill chance at round 4

Now we're talking! At 12 vs. 18 Chi, Nemeses have a 56% chance to take the players out in round 4. This peak moves to later rounds at larger Chi values, growing to 60% at 20 Chi in round 7 (having started the fight with a whopping 40 Chi!).

At more realistic Chi values, the peak looks like this:

Player starting Chi Nemesis starting Chi Rounds elapsed Nemesis win %
4 6 1 13%
4 6 2 6%
6 9 2 46%
6 9 3 3%
8 12 2 10%
8 12 3 37%
8 12 4 1%
10 15 3 40%
10 15 4 21%
10 15 5 0.5%
12 18 3 8%
12 18 4 58%
12 18 5 11%

Player skill 4 vs. Nemesis skill 5

Player Chi = Nemesis Chi

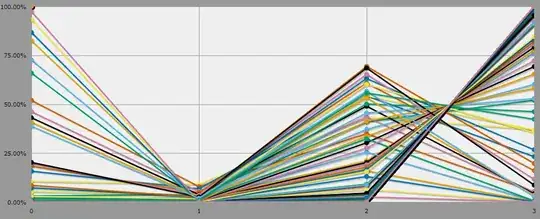
Graph indicating that Nemesis

Why would you give a Nemesis a higher skill than the good guys? Do you hate your players? ... Don't answer that.

The higher the Chi pool, the worse the outlook for the players, which makes sense: the law of large numbers always has its day.

Player starting Chi Nemesis starting Chi Rounds elapsed Nemesis win %
4 4 1 35%
4 4 2 8%
6 6 2 41%
6 6 3 3%
8 8 2 43%
8 8 3 20%
8 8 4 1%
10 10 3 54%
10 10 4 9%
12 12 3 49%
12 12 4 33%
12 12 5 4%
20 20 5 57%
20 20 6 56%
20 20 7 15%

Other values of Chi

I could include analysis of Nemesis Chi - 10% and so on here, but will not for the sake of time.

order
  • 3,865
  • 2
  • 15
  • 51