10

I know that the gold dragonborn in D&D 5e have a 15ft cone as breath weapon, but is that 15ft radius cone or 15ft diameter cone?

Someone_Evil
  • 48,298
  • 8
  • 167
  • 257
sumi
  • 221
  • 2
  • 5

2 Answers2

20

15' long, 15' wide at the end

Cones are described in the PHB (p. 204) at the end of Chapter 10 under spellcasting:

A cone extends in a direction you choose from its point of origin. A cone's width at a given point along its length is equal to that point's distance from the point of origin. A cone's area of effect specifies its maximum length.

A cone's point of origin is not included in the cone's area of effect, unless you decide otherwise.

While confusing because this is under spellcasting and the Dragonborn doesn't use a spell to do this, the mechanics of cones/lines/cubes/cylinders/spheres all rely on the mechanics described in that section.

And in this case, Width is the same as Diameter.

Community
  • 1
NotArch
  • 125,044
  • 39
  • 506
  • 804
12

A cone has a height (length) equal to its diameter (width)

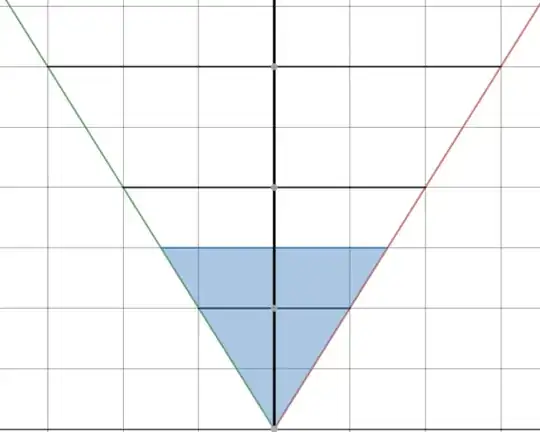
The math words and terms might get a bit complicated and strange so below is a picture of a cone satisfying these constraints (assume that each square on the grid is a 5-foot by 5-foot square) enter image description here

A vertical line extends from the cone's point of origin (at the bottom). At any point along this line you are a certain distance from the point of origin. That same distance is how "wide" your cone needs to be. For example, going from the point of origin along the vertical line until we reach the first black line requires us to move 10 feet (two squares). Thus the diameter/width of the cone at that point is also 10 feet; this is accomplished by moving five feet in all perpendicular directions. Similarly, if we move until we are four squares away from the point of origin then the cone will have a diameter of four squares, two in each direction.

Thus the 15-foot cone in question would be found by moving three squares away from the point of origin and then moving 1.5 squares in both directions. This is outlined in blue.

Note also that the cone pictured here is two-dimensional while in reality the cone would be three-dimensional. Though using cones fully in three-dimensions gets quite confusing as the line extending from the point of origin need not be parallel to the ground.

Exempt-Medic
  • 75,986
  • 11
  • 289
  • 534
  • 1
    You may want to also note that your image is 2d, but the cone is not. – NotArch Apr 06 '20 at 18:53
  • 1
    @NautArch I mentioned it but I hesitate about 3-d cones... You can change the angle that the cone is, well, angled at, such as firing it straight up or at a 45-degree angle and it gets a bit messy. The optimal "cone-aiming angle" will never be perpendicular to the ground because some slight incline might include more squares in its area without losing any squares at the same time – Exempt-Medic Apr 06 '20 at 19:06
  • FWIW, I don't believe any incline can include more squares for the ground plane (which is the only one we typically care about) than parallel to that ground. The slice for that incline is just a narrower cone. – Cireo Apr 07 '20 at 17:54
  • @Cireo That's true but if we're already talking about the three-dimensionality of the cone I assume we for some reason care about squares not on the ground plane – Exempt-Medic Apr 07 '20 at 19:25