Ignore the actual order things are done, use an order that's easier to calculate, and don't be scared to approximate
Instead of first rolling stats and then rerolling if there aren't two 15+s, we can achieve exactly the same result by first rolling two stats that must be 15+ and then rolling the rest 'normally'.
To do this in anydice, what we want to do is take the collection of possible outcomes that is what 'highest 3 of 4d6' means and just remove all the parts that are under 15.
The easiest way to do this is manually. Looking at the results of the aforementioned distribution, we can see that '15' has a 10.11% chance of occurring, '16' a 7.25% chance, '17' a 4.17% chance, and '18' a 1.62% chance. These odds are truncated to the hundredths place, but we are going to consider that level of error acceptable. A sequence with 1011 '15's, 725 '16's, 417 '17's, and 162 '18's, then, can function as a die that gives us our two best values.
Using repetition, we can populate a sequence by using the following code:
output {15:1011,16:725,17:417,18:162}
Next, we need to fix your code. It doesn't actually get you what you are looking for, I think, since it has an approximately infinitessimal chance of outputting numbers lower than 8. That may be fine with you, but we can also use truncation to get a (in my opinion) much cleaner and about equally accurate system for the remaining 4 ability scores:
output {8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162}
You can do something like output [highest 1 of 6d {8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162}] to confirm that it gives the same results.
To look at each ability score, we can just pull the appropriate number from a set of rolls, remembering that the rolls higher than 8 instead of 15 are also no better than the 3rd highest roll of such a sequence. So we end up with:
output [highest 1 of 2d{15:1011,16:725,17:417,18:162}] named "highest stat"
output 2 @ 2d{15:1011,16:725,17:417,18:162} named "2nd highest stat"
output 3@6d{8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162} named "highest non-forced stat"
output 4@6d{8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162} named "2nd highest non-forced stat"
output 5@6d{8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162} named "2nd lowest stat"
output 6@6d{8:478,9:702,10:941,11:1142,12:1289,13:1327,14:1235,15:1011,16:725,17:417,18:162} named "lowest stat"
Which gives results within 1 percentage point of the analytic value 1(approximately 10% error).
- thanks to @Carcer for the analytic value program.
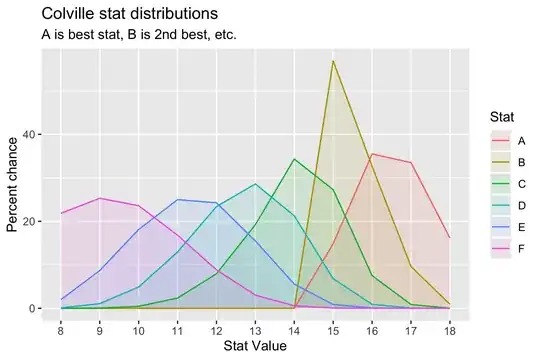
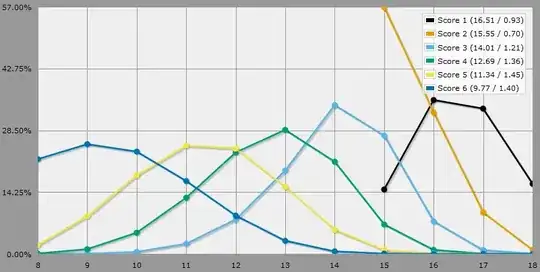
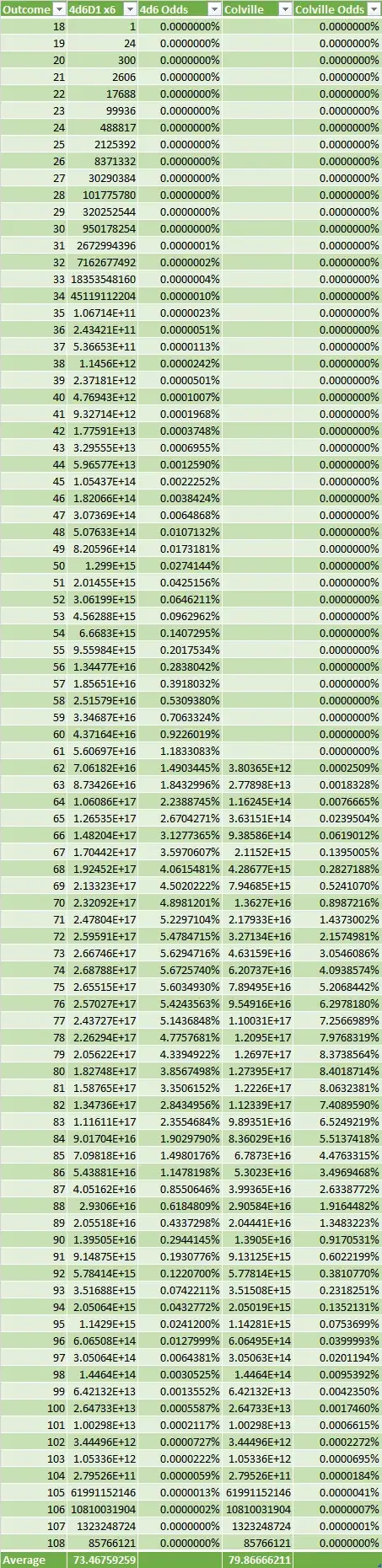
Regarding the 8s and above, the code guarantees nothing under 8 is rolled. The tables and graphs confirm it.
– Bogdan Ionică Sep 17 '19 at 13:31