At high temperatures, do planets glow like blackbodies?

Question

I've been messing around in Universe Sandbox for a while and noticed that as a planet heats up, it glows like a blackbody starting at ~4000 K. Is the simulation here accurate, or do very hot planets glow differently based on their composition?

Answer 1

At high temperatures, do planets glow like blackbodies?

Yes, and at low temperatures too!¹

¹As @DavidHammen points out, since there's likely going to be a star nearby the planet, it will also be reflecting light from it, so the "glowing" with thermal radiation may in some cases be masked or at least mixed with reflected thermal radiation from the star.

But as far as I know, when thermal infrared telescopes spot asteroids, they are seeing the asteroid's own thermal "glowing", not reflected thermal IR from the Sun.

To address this more fully I've just asked When thermal infrared space telescopes spot asteroids, are they seeing the body's own thermal emission, or reflected TIR from the Sun?

---

This is a really interesting interdisciplinary question and as this is too long for a comment I'll write something here.

A black body is an idealized concept. It's too long to quote in full but at a temperature $T$ its emission spectrum is given by Planck's law:

$$B(\nu, T) = \frac{2 h \nu^3}{c^2} \frac{1}{\exp \left(\frac{h \nu}{k_B T} \right) - 1}$$

or

$$B(\lambda, T) = \frac{2 h c^2}{\lambda^5} \frac{1}{\exp\left(\frac{h c}{\lambda k_B T}\right) - 1}$$

where $h$, $c$ and $k_B$ are the Planck constant, the speed of light and the Boltzmann constant.

Their peaks are at slightly different colors because they are differentials (i.e. per unit frequency vs per unit wavelength).

Now we are familiar with the Stefan–Boltzmann law where the total power radiated by an object of area $A$ integrated over all colors is

$$P = A \varepsilon \sigma T^4$$

where $\sigma$ is the Stefan–Boltzmann constant and $\varepsilon$ is the emissivity of the surface.

If you wanted to know the thermal emission spectrum of a body you'd multiply the Planck distribution $B$ of an idealized black body by the object's emissivity $\varepsilon$.

But wavelength-dependent emissivity is what you're really after

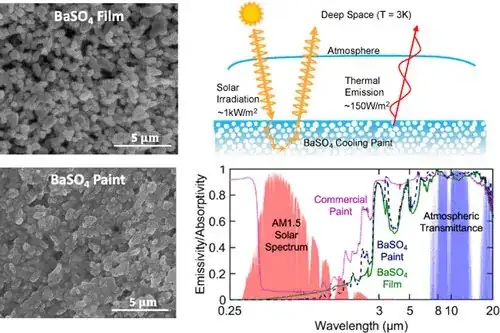
The primary way that a hot planet will deviate from a Planck distribution is in $\varepsilon$ and especially its variation with wavelength (which they often forget to tell you about in class); $\varepsilon(\nu)$ or $\varepsilon(\lambda)$.

Extreme example of wavelength-dependent emissivity

There was a recent announcement of a special "ultrawhite" paint which had extremely high albedo (97.6%, and therefore low emissivity) in the visible and a very low albedo (high emissivity; ~96%) in the "sky window" of thermal infrared.

If you painted this on something, it could potentially cool itself even in daytime by radiating heat into the "cold of space" through the sky window wavelength range where our atmosphere is somewhat transparent to thermal IR.

Source ACS Applied Materials & Interfaces @ACS_AMI tweet

Slightly related trivia

In the case of asteroids and dwarf planets (things with solid surfaces and no optically appreciable atmosphere) and especially for those too small to resolve their size, we often assume their visible albedo is low, something like 0.1 if we have no other information.

Their emissivity in thermal infrared is often assumed to be of order 0.9-ish, and that's important since space telescopes that hunt for NEOs (some up there already and ones that haven't yet got off the ground) use thermal IR to spot NEOs against a cold CMB background.

But the wavelength-dependent emissivity will show up as a deviation from a Planck distribution, and that can offer some clues as to composition (e.g. much tholins vs not so much tholins)

Why the thermal imaging of Mercury's surface requires a telescope on a jet flying through an eclipse? describes an example of using the surface brightness of an object falling within a wide band of thermal infrared wavelengths to determine its temperature. What they are doing is assuming some constant emissivity or, being NASA, maybe they factored in a previously wavelength-dependent emissivity from spectroscopy during analysis; the camera itself probably doesn't have spectral capabilities.

If you buy an infrared thermometer it either has a pre-programmed constant emissivity of like 0.9 or 0.95 or it lets you change it. The ones they stick in your ear or at your forehead are preprogrammed.