Fagure hipercubic
În geometrie, un fagure hipercubic este o familie de faguri regulați (teselări) în n-dimensiuni cu simbolurile Schläfli {4,3,...,3,4} și având simetriile grupului Coxeter Rn (sau B~n-1) pentru n ≥ 3.
 Pavare pătrată regulată 1 culoare |
 Fagure cubic regulat 1 culoare |
 Pavare pătrată tablă de șah 2 culori |
 Fagure cubic tablă de șah 2 culori |
 Pavare pătrată expandată 3 culori |
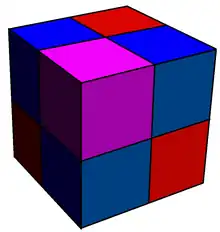 Fagure cubic expandat 4 culori |
 4 culori |
 8 culori |
Teselarea este construită cu 4-hipercuburi pe latură. Figura vârfului este un ortoplex {3,...,3,4}.
Fagurii hipercubici sunt autoduali.
Coxeter a notat această familie cu δn+1 pentru un fagure n-dimensional.
Construcția Wythoff a claselor în funcție de dimensiuni
Construcția Wythoff este o metodă de a construi un poliedru uniform sau o pavare plană.
Cele două forme generale ale fagurilor hipercubici sunt formele regulate, cu fațete hipercubice identice și unele semiregulate, fațetele alternând, ca tabla de șah.
A treia formă este generată de o formă expandată, operație care, aplicată formelor regulate, generează fațete în locul tuturor elementelor de dimensiuni inferioare. De exemplu, un fagure cubic expandat are celule cubice centrate pe cuburile originare, pe fețele originare și pe vârfurile originare, creând celule de 4 culori în jurul unui vârf vertex, în raporturile 1:3:3:1.
Fagurii ortotopici sunt o familie echivalentă topologic cu fagurii cubici, dar cu mai puține simetrii, în care dimensiunea laturilor diferă pentru fiecare din cele trei direcții axiale. Fațetele sunt hiperdreptunghiuri(d) (ortotopuri); în 2 și 3 dimensiuni ortotopurile sunt dreptunghiuri, respectiv paralelipipede dreptunghice.
| δn | Nume | Symboluri Schläfli | Diagramă Coxeter | ||
|---|---|---|---|---|---|
| Ortotopic ({∞}n) (2m culori, m < n) |
Regulat (expandat) {4,3n–1,4} (1 culoare, n culori) |
În „șah” {4,3n–4,31,1} (2 culori) | |||
| δ2 | Apeirogon | {∞} | |||
| δ3 | Pavare pătrată | {∞}2 {4,4} |
|||
| δ4 | Fagure cubic | {∞}3 {4,3,4} {4,31,1} |
|||
| δ5 | 4-fagure cubic | {∞}4 {4,32,4} {4,3,31,1} |
|||
| δ6 | 5-fagure cubic | {∞}5 {4,33,4} {4,32,31,1} |
|||
| δ7 | 6-fagure cubic | {∞}6 {4,34,4} {4,33,31,1} |
|||
| δ8 | 7-fagure cubic | {∞}7 {4,35,4} {4,34,31,1} |
|||
| δ9 | 8-fagure cubic | {∞}8 {4,36,4} {4,35,31,1} |
|||
| δn | n-fagure hipercubic | {∞}n {4,3n-3,4} {4,3n-4,31,1} |
... | ||
Note
Bibliografie
- en H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8
- pp. 122–123. (The lattice of hypercubes γn form the cubic honeycombs, δn+1)
- pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- p. 296, Table II: Regular honeycombs, δn+1
Legături externe
 Materiale media legate de fagure hipercubic la Wikimedia Commons
Materiale media legate de fagure hipercubic la Wikimedia Commons
| Faguri convecși regulați și uniformi în dimensiunile 2–8 | ||||||
|---|---|---|---|---|---|---|
| Spațiu | Familia | / / | ||||
| E2 | Pavare uniformă | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonală |
| E3 | Fagure convex uniform | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | 4-fagure uniform | {3[5]} | δ5 | hδ5 | qδ5 | Fagure 24-celule |
| E5 | 5-fagure uniform | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | 6-fagure uniform | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | 7-fagure uniform | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | 8-fagure uniform | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| En-1 | (n−1)-fagure uniform | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
