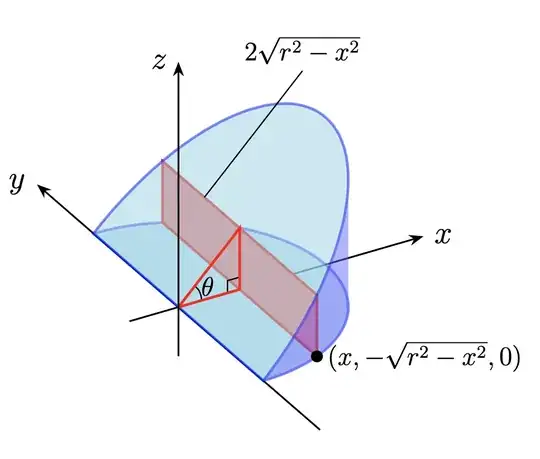
I want to draw the follwing figure in TikZ.

Of course, I was able to draw most of its components, but I can not draw the cylindrical part. Here is my effort so far.
MWE:
\documentclass[14pt]{memoir}
\usepackage{tikz, tikz-3dplot}
\usetikzlibrary{arrows.meta}
\begin{document}
\tdplotsetmaincoords{60}{-30}
\begin{tikzpicture}[tdplot_main_coords, scale=0.9]
\tdplotsetrotatedcoords{0}{45}{0}
\pgfmathsetmacro{\r}{3}
\pgfmathsetmacro{\x}{1.25}
\pgfmathsetmacro{\y}{sqrt(\r^2-\x^2)}
\draw [thick, -Stealth] (-1,0,0) -- (5,0,0) node [right] {$x$};
\draw [thick, -Stealth] (0,-5,0) -- (0,5,0) node [left] {$y$};
\filldraw [fill=cyan!40, very thick, draw=blue, canvas is xy plane at z=0, opacity=0.5] (0,-\r) arc [start angle=-90, end angle=90, radius=\r] -- cycle;
\filldraw [fill=red!50, very thick, draw=red, canvas is yz plane at x=\x] (-\y,0) rectangle (\y,\x);
\begin{scope}[tdplot_rotated_coords]
\filldraw [fill=cyan!40, very thick, draw=blue, canvas is yz plane at x=0, opacity=0.5] (\r,0) arc [start angle=0, end angle=180, x radius=\r, y radius=\r*sqrt(2)] -- cycle;
\end{scope}
\begin{scope}[canvas is xz plane at y=0]
\draw [semithick] (\x-0.25,0) -- (\x-0.25,0.25) -- (\x,0.25);
\draw [semithick] (0.47,0) arc [start angle=0, end angle=45, radius=0.47];
\node [font=\small] at (22.5:0.65) {$\theta$};
\draw [red, very thick] (0,0) -- (\x,\x) -- (\x,0) (\x,0) -- (0,0);
\end{scope}
\draw [thick, -Stealth] (0,0,-1) -- (0,0,5) node [left] {$z$};
\fill (\x,-\y,0) circle [radius=3pt];
\node [right, font=\small] at (\x,-\y,0) {$(x,-\sqrt{r^2-x^2},0)$};
\draw [semithick, font=\small] (\x,1.25,\x) --++ (2,0,2) node [above, inner sep=1mm] {$2\sqrt{r^2-x^2}$};
\end{tikzpicture}
\end{document}
and its output:
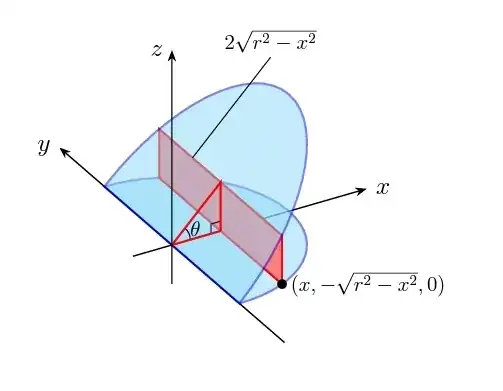 How can I complete this figure? Any help would be appreciated!
How can I complete this figure? Any help would be appreciated!
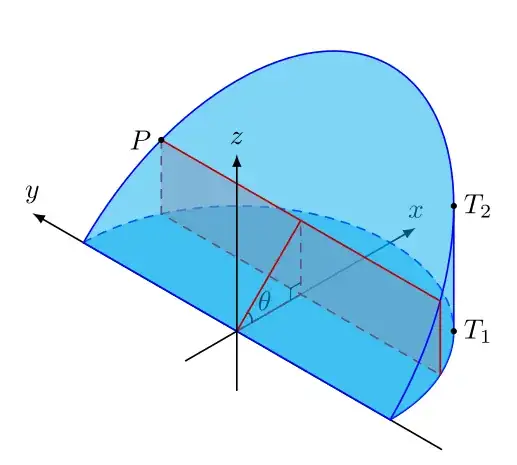
The photo mentioned in my comment in the @user241266 's answer