Log or square-root transformation for ARIMA

Question

With the below dataset, I have a series which needs transforming. Easy enough. However, how do you decide which of the SQRT or LOG transformations is better? And how do you draw that conclusion?

x<-c(75800,54700,85000,74600,103900,82000,77000,103600,62900,60700,58800,134800,81200,47700,76200,81900,95400,85400,84400,103400,63000,65500,59200,128000,74400,57100,75600,88300,111100,95000,91500,111400,73700,72800,64900,146300,83100,66200,101700,100100,120100,100200,97000,120600,88400,83500,73200,141800,87700,82700,106000,103900,121000,98800,96900,115400,87500,86500,81800,135300,88900,77100,109000,104000,113000,99000,104500,109400,92900,88700,90500,140200,91700,78800,114700,100700,113300,122800,117900,122200,102900,85300,92800,143800,88400,75400,111200,96300,114600,108300,113400,116600,103400,87300,88200,149800,90100,78800,108900,126300,122000,125100,119600,148800,114600,101600,108800,174100,101100,89900,126800,126400,141400,144700,132800,149000,124200,101500,106100,168100,104200,79900,126100,121600,139500,143100,144100,154500,129500,109800,116200,171100,106700,85500,132500,133700,135600,149400,157700,144500,165400,122700,113700,175000,113200,94400,138600,132400,129200,165700,153300,141900,170300,127800,124100,206700,131700,112700,170900,153000,146700,197800,173800,165400,201700,147000,144200,244900,146700,124400,168600,193400,167900,209800,198400,184300,214300,156200,154900,251200,127900,125100,171500,167000,163900,200900,188900,168000,203100,169800,171900,241300,141400,140600,172200,192900,178700,204600,222900,179900,229900,173100,174600,265400,147600,140800,171900,189900,185100,218400,207100,178800,228800,176900,170300,251500,149900,150300,192000,185100,184500,228800,219000,180000,241500,184300,174600,264500,166100,151900,194600,214600,201700,229400,233600,197500,254600,194000,201100,279500,175800,167200,235900,207400,215900,261800,236800,222400,281500,214100,218200,295000,194400,180200,250400,212700,251300,280200,249300,240000,304200,236900,232500,300700,207300,196900,246600,262500,272800,282300,271100,265600,313500,268000,256500,318100,232700,198500,268900,244300,262400,289200,286600,281100,330700,262000,244300,309300,246900,211800,263100,307700,284900,303800,296900,290400,356200,283700,274500,378300,263100,226900,283800,299900,296000,327600,313500,291700,333000,246500,227400,333200,239500,218600,283500,267900,294500,318600,318700,283400,351600,268400,251100,365100,249100,216400,245500,232100,236300,275600,296500,296900,354300,277900,287200,420200,299700,268200,329700,353600,356200,396500,379500,349100,437900,350600,338600,509100,342300,288800,378400,371200,395800,450000,414100,387600,486600,355300,358800,526800,346300,295600,361500,415300,402900,484100,412700,395800,491300,391000,374900,569200,369500,314900,422500,436400,439700,509200,461700,449500,560600,435000,429900,633400,417900,365700,459200,466500,488500,531500,483500,485400,575700,458000,433500,642600,409600,363100,430100,503900,500400,557400,565500,526700,628900,547700,520400,731200,494400,416800,558700,537100,556200,686700,616600,582600,725800,577700,552100,806700,554200,455000,532600,693000,619400,727100,684700)
y<-ts(x,frequency=12, start=c(1976,1))
#Transforming the data to log or sqrt and plotting it
log.y<-log(y)
plot(log.y)
sqrt.y<-sqrt(y)
plot(sqrt.y)

Answer 1

This question is answered beautifully by means of a spread-versus-level plot: a cube root transformation will stabilize the spreads of the data, providing a useful basis for further exploration and analysis.

---

The data show a clear seasonality:

plot(y)

Take advantage of this by slicing the data into annual (or possibly biennial) groups. Within each group compute resistant descriptors of their typical value and their spread. Good choices are based on the 5-letter summary, consisting of the median (which splits the data into upper and lower halves), the medians of the two halves (the "hinges" or "fourths"), and the extremes. Because the extremes are not resistant to outliers, use the difference of the hinges to represent the spread. (This "fourth-spread" is the length of a box in a properly constructed box-and-whisker plot.)

spread <- function(x) {
  n <- length(x)
  n.med <- (n + 1)/2
  n.fourth <- (floor(n.med) + 1)/2
  y <- sort(x)[c(floor(n.fourth), ceiling(n.fourth), 
               floor(n+1 - n.fourth), ceiling(n+1 - n.fourth))]
  return( y %*% c(-1,-1,1,1)/2 )
}
years <- floor((1:length(x) - 1) / 12)
z <- split(x, years)
boxplot(z, names=(min(years):max(years))+1976, ylab="y")

The boxplots clearly get longer over time as the level of the data rises. This heteroscedasticity complicates analyses and interpretations. Often a power transformation can reduce or remove the heteroscedasticity altogether.

A spread versus level plot shows whether a power transformation (which includes the logarithm) will be helpful for stabilizing the spread within the groups and suggests an appropriate value for the power: it is directly related to the slope of the spread-vs.-level plot on log-log scales.

z.med <- unlist(lapply(z, median))
z.spread <- unlist(lapply(z, spread))
fit <- lm(log(z.spread) ~ log(z.med))
plot(log(z.med), log(z.spread), xlab="Log Level", ylab="Log Spread", 
     main="Spread vs. Level Plot")
abline(fit, lwd=2, col="Red")

This plot shows good linearity and no large outliers, attesting to a fairly regular relationship between spread and level throughout the time period.

When the fitted slope is $p$, the power to use is $\lambda=1-p$. Upon applying the suggested power transformation, the spread is (approximately) constant regardless of the level (and therefore regardless of the year):

lambda <- 1 - coef(fit)[2]
boxplot(lapply(z, function(u) u^lambda), names=(min(years):max(years))+1976, 
        ylab=paste("y^", round(lambda, 2), sep=""),
        main="Boxplots of Re-expressed Values")

plot(y^lambda, main= "Re-expressed Values", ylab=paste("y^", round(lambda, 2), sep=""))

Often, powers that are reciprocals of small integers have useful or natural interpretations. Here, $\lambda = 0.32$ is so close to $1/3$ that it may as well be the cube root. In practice, one might choose to use the cube root, or perhaps round it to the even simpler fraction $1/2$ and take the square root, or sometimes go all the way to the logarithm (which corresponds to $\lambda = 0$).

---

Conclusions

In this example, the spread-versus-level plot (by virtue of its approximate linearity and lack of outliers) has shown that a power transformation will effectively stabilize the spread of the data and has automatically suggested the power to use. Although powers can be computed using various methods, none of the standard methods provides the insight or diagnostic power afforded by the spread-versus-level plot. This should be in the toolkit of every data analyst.

---

References

Tukey, John W. Exploratory Data Analysis. Addison-Wesley, 1977.

Hoaglin, David C., Frederick Mosteller, and John W. Tukey, Understanding Robust and Exploratory Data Analysis. John Wiley and Sons, 1983.

Answer 2

Transformations are like drugs ! Some are good for you and some aren't !. Haphazard selection of transformations should be studiously avoided.

a) One of the requirements in order to perform valid statistical tests of necessity is that the variance of the errors from the proposed model must not be proven to be non-constant. If the variance of the errors changes at discrete points in time then one has recourse to Generalized Least Squares or GLM .

b) If the variance of the errors is linearly relatable to the level of the observed series then a Logarithmic Transformation might be appropriate. If the square root of the variance of the errors is linearly relatable to the level of the original series then a Square Root transformation is appropriate. More generally the appropriate power transformation is found via the Box-Cox test where the optimal lambda is found. Note that the Box-Cox test is universally applicable and doesn't soley requite time series or spatail data.

All of the above ( a and b ) require that the mean of the errors cannot be proven to differ significantly from zero for all points. If your data is not time series or spatial in nature then the only anomaly you can detect is a pulse. However if your data is time series or spatial then Level Shifts , Seasonal Pulses and/or Local Time Trends might be suggested to render the mean value of the error term to be 0.0 everywhere or at least not significantly different from 0.0 .

In my opinion one should never willy-nilly transform the data unless one has to in order to satisfy (in part) the Gaussian assumptions. Some econometricians take logs for the simple and simply wrong reason in order to obtain direct estimates of elasticity's rather than assessing the % change in Y for a % change in x from the best model.

Now one caveat, if one knows from theory or at least one thinks that one knows from theory that transformations are necessary i.e. proven by previous well-documented research , then by all means follow that paradigm as it may prove to be more beneficial that the empirical procedures I have laid out here.

In closing use the original data, minimize any warping of the results by mindless transformations, test all assumptions and sleep well at night. Statisticians like Doctors should never do harm to their data/patients y providing drugs/transformations that have nasty and unwarranted side-effects.

Hope This Helps .

Data Analysis using time series techniques on time series data:

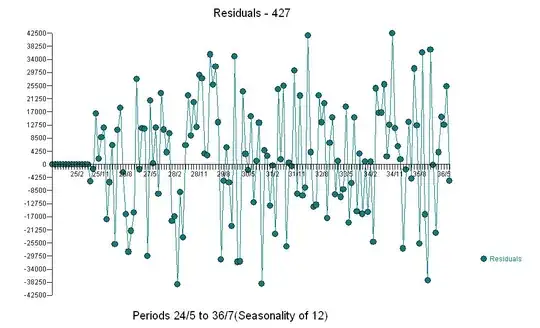a plot suggests a series that has structural change. The Chow Test yielded a signifciant break point . . Analysis of the modt recent 147 values starting at 1999/5 yielded with a Residual Plot with the following ACF . The forecast plot is . The final model is with all parameters statistically significant and no unwarranted power transformations which often unfortunately lead to wildly explosive and unrealistic forecasts. Power transforms are justified whrn it is proven via a Box-Cox test that the variablility of the ERRORS is related to the expected value as detailed here. N.B. that the variability of the original series is not used but the variability of model errors.

Answer 3

@digdeep, as usual @whuber provided an excellent and comprehensive answer from a statistical view point. I'm not trained in statistics, so take this response with a grain of salt. I have used the response below in my real world practice data, so I hope this is helpful.

I'll try to provide a non statistician view of transformation of time series data for Arima modeling. There is no straightforward answer. Since you are interested in knowing which transformation to use, it might be helpful to review why we do transformation.We do transformation for 3 main reasons and there might be ton of other reasons:

1. Transformation makes the data's linear structure more usable for
   ARIMA modeling.
2. If variance in the data is increasing or changing then transformation of data might be helpful to stabilize the variance in data.
3. Transformation also makes the errors/residuals in ARIMA model normally distributed which is a requirement in ARIMA modeling proposed by Box-Jenkins.

There are several data transformations including Box-Cox, Log, square root, quartic and inverse and other transformations mentioned @irishstat. As with all the statistical methods there is no good guidance/answer on which transformation to select for a particular dataset.

As the famous statistician G.E.P Box said "All models are wrong but some are useful", this would apply to the transformations as well "All transformations are wrong but some are useful".

The best way to choose a transformation is to experiment. Since you have a long time series, I would hold out the last 12 - 24 months, and build a model using all the transformation and see if a particular transformation is helpful at predicting your out of sample data accurately. Also examine the residuals for normality assumption of your model. Hopefully, this would guide you in choosing an appropriate transformation. You might also want to compare this with non-transformed data and see if the transformation helped your model.

@whuber's excellent graphical representation of your data motivated me to explore this data graphically using a decomposition method. I might add, R has an excellent decomposition method called STL which would be helpful in identifying patterns that you would normally not notice. For a dataset like this, STL decomposition is helpful in not only selecting an appropriate method for analyzing your data, it might also be helpful in identifying anomalies such as outliers/level shift/change in seasonality etc., See below. Notice that the remainder (irregular) component of the data, looks like there is stochastic seasonality and the variation is not random, there appears to be a pattern. See also change in level of trend component after 2004/2005 that @whuber is refrencing.

Hopefully this is helpful.

g <- stl(y,s.window = "periodic")
plot(g)