We have a study setup for testing a new learning treatment, which basically looks like this:
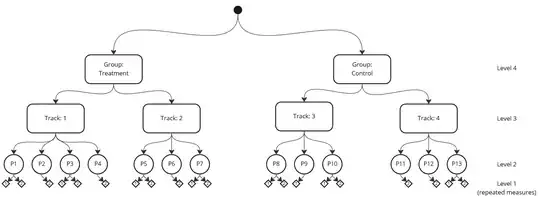
We have 4 tracks (same university course taught by different lecturers). In two of these tracks, the lecturers follow a new procedure (use of a digital learning enviroment), while in the other two, the lecturers teach as usual using whiteboard etc. (control group). The tracks have approximately 14 to 33 students each (P1 etc. in the graphic). The students chose the tracks themselves, so the tracks are not properly randomized as students could choose a track for whatever reasons (preferred lecturer, preferred time etc.). The students did a pre- and a post test (for measuring learning gains), though due to students arriving late and leaving early, not all students did both pre- and post-test.
Our hypothesis testing is mainly concerned with the effect of the treatment, but if possible we somehow want to consider the effect of the track itself (e.g. the experience of the lecturer, the time of the course etc.).
Our questions thus are:
- The nested variables
groupandtrackare colinear.groupis basically a function oftrack. When using linear models, the advice for such sitations seems to be to remove the higher-level variable as it is redundant. But how could we do our hypothesis test about the treatment, if we remove the according variable from the linear model? - Alternatively, it seems a mixed effects model could be used, treating
trackas a random effect. Reading up on it though, it seems that the grouping levels should have at least 5 to 6 samples, which is clearly not the case in this situation. - What would be the best statistical model for such a situation? Should tracks just be ignored as a level and the treatment and control group be compared directly? Should such a test simply be accompanied by extra tests (e.g. pairwise comparisons between all tracks)?
Thank you very much!