QQ plot result doesn't correspond to normality test

Question

I am considering an ANOVA model for such data:

Student    Class  Points on exam   Day of studying
1           P1       12             Day 10
2           P3       23             Day 5
3           P3       8              Day 1
4           P2       36             Day 10
5           P1       10             Day 1
6           P2       86             Day 10
7           P1       13             Day 5
...

and such ANOVA model:

model <- aov(Points ~ Class + Day, data)
ggqqplot(residuals(model))

how can I check if this model satisfies the normality of distribution? (other than the Q-Q plot of the model?)

My Q-Q plot of the model (above) seems to show normal distribution but when I perform Shapiro-Wilk( that considers only Points) the p-value comes out incredibly small... Therefore I don't know if I can assume the normality or not.

Shapiro-Wilk normality test
data:  Points
W = 0.92212, p-value = 9.97e-13

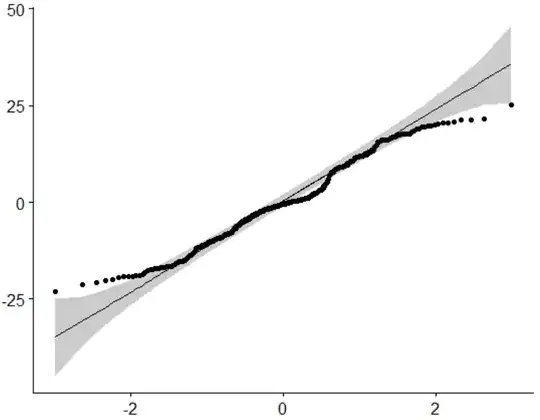
"My Q-Q plot of the model (above) seems to show normal distribution". Does it? — statsplease, May 22 '22 at 06:46
The only normal quantile plot of interest here is of the residuals. Is that what you are showing. A plot of the "model" could be many things. (I am not a routine R user but in any case if I understand correctly you don't show the syntax used to produce the plot. — Nick Cox, May 22 '22 at 08:37
Thanks for the clarification. So, compare like with like: Shapiro-Wilk on the residuals will I guess reject overwhelmingly too, but that doesn't mean much. The real issue is whether these results point to a different analysis, which I doubt. You have Points and at least 3 classes and at least 3 days. Unless the distribution of Points is. conditional, on predictor, very skewed I doubt there is a strong case for doing anything different. The threads cited by @Tim are helpful here. — Nick Cox, May 22 '22 at 09:50

Tim · Answer 1 · 2022-05-22T07:29:26.870

Your Q-Q plot does not show that the data is normally distributed. In fact, it shows that the distribution diverges from Gaussian (values lower than -1 and higher than 1.5 diverge from the diagonal dashed line). See also the Interpreting QQplot - Is there any rule of thumb to decide for non-normality? thread.
You may be also interested in the Is normality testing 'essentially useless'? thread. Are those normality tests really needed? Likely not.

score 4 · Answer 2 · answered May 22 '22 at 06:57

4

Just on first look, this distribution looks very short tailed, as you can see it looks kind of like this simulation with a uniform distribution

answered May 22 '22 at 06:57

PhysicsKid

190

QQ plot result doesn't correspond to normality test

2 Answers2