I am doing a simple neural network regression and I notice my predictions always have high variation at the edges (values 0 and 1, in a normalized case). An image of the true value versus predicted is as shown here:
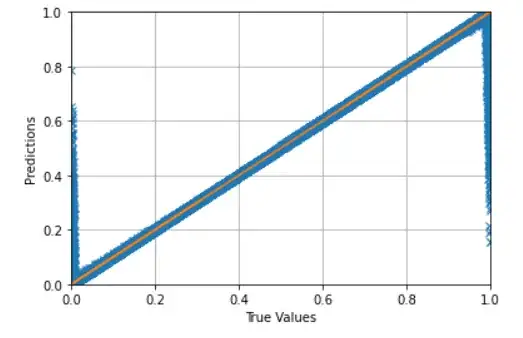
I am using linear activation as the output activation function, and I cannot fathom what could cause this. Can anyone suggest A) what causes this? and B) what could be done to avoid this?
I see similar post here, but can't say I understand the answer provided: Shape of confidence interval for predicted values in linear regression