Is it possible to test more rats? The treatment cured one rat and controlled the tumour growth of two other rats, so you have evidence the treatment is successful. But the variance in the treatment outcome is high: how often does the treatment cure vs control the tumour?
There is no agreement on how many subjects per factor you need to fit a random-effects model. You can read more here; in short the advice is to have at least six levels to estimate a random effect. In your experiment, this means at least six rats (per treatment group).
Now about interpreting the results from your model. You fit a random-intercept random-slope model for the log of tumour size and you are interested in the fixed effect treatment vs control over time.
I suspect that you've added 1 to Size in order to take the log transform (and that's why Size decreases to 1 for lucky Rat4 and then doesn't change further). Instead it might be better to keep the original measurements and remove those time points. At least for the data you have at hand; perhaps in general it's possible for the tumour to grow back?
Let's demonstrate: First use all data points for Rat4. Observe the poor fit after the tumour disappears.
fit <- lmer(
log(Size) ~ Group * Time + (Time | Rat),
data = DF1
)

And now the same model but we exclude the Size = 1 data points for Rat4 (except the first such observation). Now the treatment intercept is higher and the slope is a tiny bit steeper.
fit <- lmer(
log(Size) ~ Group * Time + (Time | Rat),
data = DF1 %>% group_by(Rat) %>% filter(cumsum(Size == 1) < 2)
)

Now let's see the marginal effect of Treatment over time. There is evidence that the treatment is effective because tumour size is smaller for DrugA than it is for Control after about 2 weeks. However, the confidence intervals are probably not correct as the variance is not modelled well as I discuss below.
library("ggeffects")
ggeffect(fit, terms = c("Time", "Group"))
#> # Predicted values of Size
#>
#> # Group = Control
#>
#> Time | Predicted | 95% CI
#> -------------------------------
#> 0 | 4.62 | [4.16, 5.08]
#> 14 | 4.91 | [4.68, 5.14]
#> 28 | 5.20 | [4.61, 5.80]
#> 42 | 5.49 | [4.43, 6.55]
#> 56 | 5.78 | [4.25, 7.32]
#> 84 | 6.37 | [3.87, 8.86]
#>
#> # Group = DrugA
#>
#> Time | Predicted | 95% CI
#> -------------------------------
#> 0 | 4.68 | [4.21, 5.14]
#> 14 | 4.33 | [4.10, 4.56]
#> 28 | 3.99 | [3.39, 4.58]
#> 42 | 3.64 | [2.58, 4.70]
#> 56 | 3.30 | [1.76, 4.83]
#> 84 | 2.61 | [0.11, 5.10]
You can get the estimated marginal mean Size (as a function of Time) from the model summary as well.
Betas <- fixef(fit)
Time <- seq(0, 84, by = 7)
Expected log(size) for an untreated rat over Time
Control_intercept <- Betas["(Intercept)"]
Control_slope <- Betas["Time"]
Control_intercept + Control_slope * Time
#> [1] 4.62 4.77 4.91 5.06 5.20 5.35 5.49 5.64 5.78 5.93 6.08 6.22 6.37
Expected log(Size) for a treated rat over Time
DrugA_intercept <- Betas["(Intercept)"] + Betas["GroupDrugA"]
DrugA_slope <- Betas["Time"] + Betas["GroupDrugA:Time"]
DrugA_intercept + DrugA_slope * Time
#> [1] 4.68 4.50 4.33 4.16 3.99 3.81 3.64 3.47 3.30 3.13 2.95 2.78 2.61
The model however assumes the variance in the same for the control and treated group. In practice the estimated variance is too high for Control and too low for DrugA: the confidence band is too wide for control rats (left panel) and too narrow for treated rats (right panel).
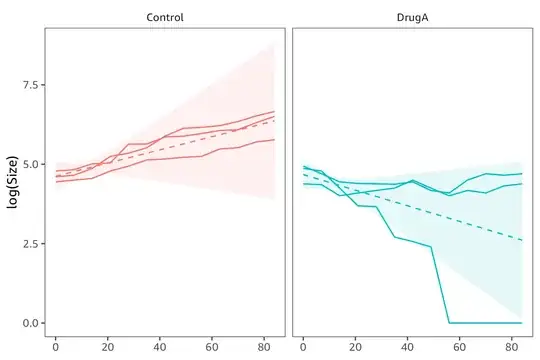
The next step would be to nest the Rat random effects within Group, so that Control and Treatment have separate variance components. See The correct random slope model for nested data.
Unfortunately you have only three rats per group, so the model fails to converge. We circle back to the fact that you would need more rats to extend the statistical analysis in a meaningful way.
You already have evidence, however, that the treatment is more effective than the control.
fit <- lmer(
log(Size) ~ Group * Time + (Time | Group / Rat),
data = DF1
)
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
#> unable to evaluate scaled gradient
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
#> Model failed to converge: degenerate Hessian with 1 negative eigenvalues
The R code to reproduce the figures:
library("lme4")
library("ggeffects")
library("tidyverse")
DF1 <- tibble::tribble(
~Rat, ~Size, ~Time, ~Group,
"Rat1", 85, 0, "Control",
"Rat1", 90, 7, "Control",
"Rat1", 95, 14, "Control",
"Rat1", 120, 21, "Control",
"Rat1", 140, 28, "Control",
"Rat1", 170, 35, "Control",
"Rat1", 175, 42, "Control",
"Rat1", 185, 49, "Control",
"Rat1", 190, 56, "Control",
"Rat1", 240, 63, "Control",
"Rat1", 250, 70, "Control",
"Rat1", 300, 77, "Control",
"Rat1", 320, 84, "Control",
"Rat2", 100, 0, "Control",
"Rat2", 105, 7, "Control",
"Rat2", 130, 14, "Control",
"Rat2", 190, 21, "Control",
"Rat2", 210, 28, "Control",
"Rat2", 250, 35, "Control",
"Rat2", 360, 42, "Control",
"Rat2", 460, 49, "Control",
"Rat2", 475, 56, "Control",
"Rat2", 500, 63, "Control",
"Rat2", 570, 70, "Control",
"Rat2", 680, 77, "Control",
"Rat2", 781, 84, "Control",
"Rat3", 120, 0, "Control",
"Rat3", 125, 7, "Control",
"Rat3", 150, 14, "Control",
"Rat3", 155, 21, "Control",
"Rat3", 280, 28, "Control",
"Rat3", 281, 35, "Control",
"Rat3", 350, 42, "Control",
"Rat3", 360, 49, "Control",
"Rat3", 390, 56, "Control",
"Rat3", 430, 63, "Control",
"Rat3", 440, 70, "Control",
"Rat3", 550, 77, "Control",
"Rat3", 670, 84, "Control",
"Rat4", 130, 0, "DrugA",
"Rat4", 120, 7, "DrugA",
"Rat4", 70, 14, "DrugA",
"Rat4", 40, 21, "DrugA",
"Rat4", 39, 28, "DrugA",
"Rat4", 15, 35, "DrugA",
"Rat4", 13, 42, "DrugA",
"Rat4", 11, 49, "DrugA",
"Rat4", 1, 56, "DrugA",
"Rat4", 1, 63, "DrugA",
"Rat4", 1, 70, "DrugA",
"Rat4", 1, 77, "DrugA",
"Rat4", 1, 84, "DrugA",
"Rat5", 140, 0, "DrugA",
"Rat5", 110, 7, "DrugA",
"Rat5", 85, 14, "DrugA",
"Rat5", 81, 21, "DrugA",
"Rat5", 80, 28, "DrugA",
"Rat5", 79, 35, "DrugA",
"Rat5", 85, 42, "DrugA",
"Rat5", 65, 49, "DrugA",
"Rat5", 60, 56, "DrugA",
"Rat5", 90, 63, "DrugA",
"Rat5", 110, 70, "DrugA",
"Rat5", 105, 77, "DrugA",
"Rat5", 110, 84, "DrugA",
"Rat6", 80, 0, "DrugA",
"Rat6", 78, 7, "DrugA",
"Rat6", 55, 14, "DrugA",
"Rat6", 60, 21, "DrugA",
"Rat6", 65, 28, "DrugA",
"Rat6", 70, 35, "DrugA",
"Rat6", 90, 42, "DrugA",
"Rat6", 70, 49, "DrugA",
"Rat6", 55, 56, "DrugA",
"Rat6", 65, 63, "DrugA",
"Rat6", 60, 70, "DrugA",
"Rat6", 75, 77, "DrugA",
"Rat6", 80, 84, "DrugA"
)
fit <- lmer(
log(Size) ~ Group * Time + (Time | Rat),
data = DF1
)
augment(fit) %>%
ggplot(
aes(
Time, .fitted,
group = Rat,
color = Group
)
) +
geom_line() +
geom_line(
aes(Time, log(Size)),
linetype = 2
) +
facet_wrap(
~Rat,
ncol = 3
) +
labs(
y = "log(Size)"
) +
theme(
axis.title.x = element_blank(),
legend.position = "none"
)
fit <- lmer(
log(Size) ~ Group * Time + (Time | Rat),
data = DF1 %>% group_by(Rat) %>% filter(cumsum(Size == 1) < 2)
)
augment(fit) %>%
ggplot(
aes(
Time, .fitted,
group = Rat,
color = Group
)
) +
geom_line() +
geom_line(
aes(Time, log(Size)),
linetype = 2
) +
facet_wrap(
~Rat,
ncol = 3
) +
labs(
y = "log(Size)"
) +
theme(
axis.title.x = element_blank(),
legend.position = "none"
)
ggeffect(fit, terms = c("Time", "Group"))
Betas <- fixef(fit)
Time <- seq(0, 84, by = 7)
Expected log(Size) for an untreated rat over Time
Control_intercept <- Betas["(Intercept)"]
Control_slope <- Betas["Time"]
round(Control_intercept + Control_slope * Time, 2)
Expected log(Size) for a treated rat over Time
DrugA_intercept <- Betas["(Intercept)"] + Betas["GroupDrugA"]
DrugA_slope <- Betas["Time"] + Betas["GroupDrugA:Time"]
round(DrugA_intercept + DrugA_slope * Time, 2)
ggeffect(fit, terms = c("Time", "Group")) %>%
as_tibble() %>%
rename(
Group = group
) %>%
ggplot(
aes(
x, predicted,
ymin = conf.low, ymax = conf.high,
group = Group
)
) +
geom_line(
aes(color = Group),
linetype = 2
) +
geom_ribbon(
aes(fill = Group),
alpha = 0.1
) +
geom_line(
aes(
Time, log(Size),
group = Rat,
color = Group
),
data = DF1,
inherit.aes = FALSE
) +
facet_wrap(
~Group,
ncol = 3
) +
labs(
y = "log(Size)"
) +
theme(
axis.title.x = element_blank(),
legend.position = "none"
)



