0

Edit: the most obvious way forward would be to convert the data to a linear form. The data below seem to be a polynomial of order five. My question is do we know of any way to convert a polynomial of order five to a linear form?

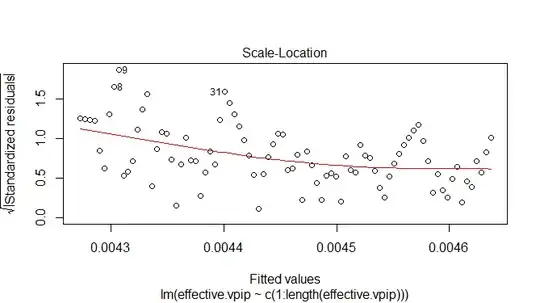
I have data for the effective changing VPIP of a poker agent over 86 hands. Need help determining if I can indeed use a linear model and if errors are normal.

  • Each data point is the average of a cumulative probability. Therefore the first data point is simply the probability of an event. The second data point is the cumulative probability of of a specific event at time 1 + an event at time 2, all divided by 2. The third data point is the cumulative prob of the events expected to happen at times 1-3 all divided by 3. Note that the "events" in question are the probabilities of a poker player receiving a one of a set of particular starting hands, where the set of starting hands increases at each time point. So the event at time 1 is the probability of getting 2 Aces (4 choose 2 divided by 52 choose 2). The event at time 2 is the player being dealt EITHER 2 Aces or 2 Kings. etc.
  • In below plots, the response variable is called effective.vpip and the x variable I havent named (is just called c(1:length(effective.vpip))

Residuals vs fitted values

NormalQQ

Standardized residuals vs fitted

Cooks plot

Other notes

  • If this turns out to be a good linear fit, then I will go on to transform the model into a dynamic linear model with drift i.e. a random walk with drift. so the linear model will be modelled as y(t)=y(t-1) + (drift term determined by slope of linear model) + (error term which is normally distributed and has time varying errors (just as in the data) which correspond to the errors of the data wrt the linear model).
user5211911
  • 31
  • 1
    This is a sequel to https://stats.stackexchange.com/questions/305946/is-it-okay-to-fit-a-linear-model-to-my-data-and-if-so-are-the-errors-normally At an absolute minimum it needed that cross-reference. Better to edit the previous question than start another -- and run the risk of people repeating themselves in comment or query. Specifically, you're not addressing points made previously. – Nick Cox Oct 03 '17 at 07:25
  • Yes, correct and my apologies. This one also has the underlying data changed, with added info – user5211911 Oct 03 '17 at 07:32
  • 2
    From what I understand, no plain or fancy regression model, linear or even quintic polynomial, either matches the set-up or can possibly add insight to analysis of a time-dependent process. Whatever they do over the range of the data, they can't match the limiting behaviour that seems evident. Sorry, but I don't know anything about poker except that it's a card game and so don't know what VPIP is or what probability model makes sense here. – Nick Cox Oct 03 '17 at 08:04

0 Answers0