Univariate clustering of time series

Question

I just want to know if its possible to cluster an univariate time series, in order , say, to detect anomalies?

and do you have any online version for denstream code, in Matlab?

---

here is the time series

+0003;+0004;+0004;+0005;+0004;+0004;+0004;+0003;+0003;+0004;+0003;+0002;+0004;+0002;+0002;+0002;+0002;+0002;+0002;+0005;+0004;+0004;+0004;+0004;+0004;+0004;+0004;+0004;+0004;+0004;+0004;+0005;+0004;+0004;+0004;+0004;+0003;+0003;+0000;+0002;+0004;+0002;+0004;+0004;+0004;+0004;+0003;+0003;+0004;+0003;+0002;+0000;+0003;+0002;+0003;+0002;+0002;+0002;+0002;+0002;+0003;+0002;+0002;+0003;+0000;+0003;+0003;+0002;+0003;+0002;+0003;+0002;+0004;+0004;+0004;+0003;+0004;+0004;+0004;+0004;+0004;+0005;+0004;+0002;+0003;+0002;+0005;+0004;+0003;+0003;+0001;+0005;+0003;+0003;+0005;+0005;+0004;+0005;+0002;+0005;+0005;+0006;+0005;+0005;+0004;+0003;+0003;+0005;+0002;+0002;+0001;+0003;+0004;+0002;+0002;+0002;+0001;+0001;+0003;+0004;+0004;+0004;+0005;+0004;+0005;+0002;+0002;+0005;+0003;+0002;+0003;+0002;+0001;+0002;+0003;+0005;+0004;+0005;+0004;+0004;+0003;+0003;+0004;+0005;+0003;+0004;+0005;+0004;+0005;+0003;+0003;+0005;+0005;+0005;+0003;+0002;+0004;+0004;+0004;+0005;+0005;+0004;+0005;+0005;+0004;+0004;+0003;+0003;+0005;+0005;+0005;+0005;+0004

---

First you should now @IrishStat, that i should use a datamining technique for clustering, an exemple of times serie dataset is presented in this :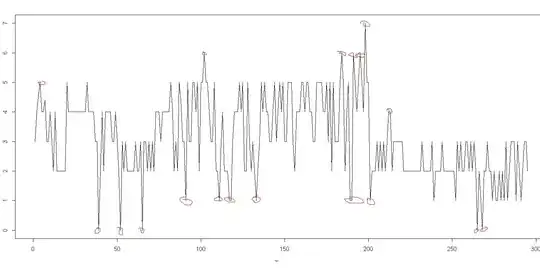

What i'm using now , is a density base clustering, let's said that I have adapte the Dbscan for streaming Time series points, and its Should detect anomalies, and changes eacht time,

after your introdudction , i'll trying to explain to u by pictures what i'm doing,

thanks u ,

time data series sample :

     [,1]
V1    3.0
V2    4.0
V3    4.5
V4    5.0
V5    4.0
V6    4.0
V7    4.4
V8    3.0
V9    3.0
V10   4.0
V11   3.0
V12   2.0
V13   4.0
V14   2.0
V15   2.0
V16   2.0
V17   2.0
V18   2.0
V19   2.0
..... so on 

Answer 1

I would approach this problem from a robust filtering point of view, as is done for real time curve monitoring. There is a German team that has worked extensively on this and related problems such as filtering, shift detection etc. --see these papers here, here and here for example--

They also have an R package were most of these algorithm are implemented in C++ and in their "on-line" versions. Check the codes in the robfilter package.

Fried R., Bernholt, T. Gather, U. (2006), Repeated median and hybrid filters, Computational Statistics & Data Analysis 50(9), 2313-2338

Fried, R., Gather, U. (2007), On Rank Tests for Shift Detection in Time Series, Computational Statistics and Data Analysis, Special Issue on Machine Learning and Robust Data Mining 52, 221-233.

Gather, U., Schettlinger, K., Fried, R. (2006), Online signal extraction by robust linear regression. Computational Statistics 21, 33-51.

Schettlinger, K., Fried, R., Gather, U. (2006), Robust Filters for Intensive Care Monitoring: Beyond the Running Median, Biomedizinische Technik 51(2), 49-56.

Answer 2

Univariate clustering is another way of looking at Intervention Detection. Unusual values (anomalies) can arise as Pulses , Seasonal Pulses or Level Shifts ( a contiguous sequence of anomalies having the same same sign and magnitude ). Consider the airline series where the anomalies are not visually obvious. A histogram of the original series and the histogram of the anomalie-cleansed series is informative. . In order to detect the statistically significant anomalies it was necessary to have a model (Note: There is no need for a logarithmic transformation as the variance of these errors is homogenous ) which yielded the following ACF for the error term . In many cases there are level shifts ( distinctly different means ) waiting to be discovered. For example the Nile Series (annual data for 100 years) is a series that illustrates this and . The histogram of the original series is naively suggests just two pulses (low values) while a model containing the empirically identified level (mean) shift generates the following analysis with model detailing the step (level ) shift and the one-time pulses . Bacon summarized this, writing in Novum Organum about 400 years ago said: "Errors of Nature, Sports and Monsters correct the understanding in regard to ordinary things, and reveal general forms. For whoever knows the ways of Nature will more easily notice her deviations; and, on the other hand, whoever knows her deviations will more accurately describe her ways." which I have paraphrased . In summary detecting anomalies require a model which describes "typical behavior". Segmenting data into "typical and "atypical" is what Intervention Detection is all about http://www.unc.edu/~jbhill/tsay.pdf and elsewhere.

ADDITIONAL ANSWER TO ACTUAL 173 VALUES

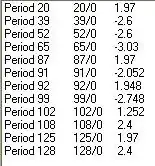Anomalies can be both one-time events (pulses) or they can be a contiguous sequence od pulses having the same sign and similar magnitude (Level/Step Shifts). You data has been identified as having an ARIMA structure ( simple AR(1) ; value .568 ) and with 12 pulses and 1 level/step shift at period 136. The identified pulses in chronological order; 1 time anomalies) . The actual step-by-step analysis started with the ACF of the original series which led to an automatically identified ARIMA model which upon estimation was reduced to . Using procedures called Intervention Detection detailed by Tsay and others http://www.unc.edu/~jbhill/tsay.pdf and a number of my previous posts here at SE led to . Now the final ACF of the errors suggesting sufficiency is . The histogram of the original 173 values is of little help in detailing the anomalies and the level/step shift DUE to the auto-correlative structure in the 173 values. .The Histogram of the final model residuals ( original series adjusted for memory, 1 level shift and the one-time pulses ) is shown . The plot of actual and cleansed provides another view . Summary: to find the exception , one needs to have an expectation.

Answer 3

I would suggest you PWCTools for MatLab from here:

Implementations of algorithms for noise removal from 1D piecewise constant signals, such as total variation and robust total variation denoising, bilateral filtering, K-means, mean shift and soft versions of the same, jump penalization, and iterated medians. It uses a range of solvers including interior-point optimization, adaptive step-size Euler integration and greedy knot placement.

It is simple to use and produces fast and robust results. In your case k-means clusterring would be the best choice although you can try other techniques depending on your needs.