I want to predict a binary response variable y using logistic regression. x1 to x4 are the log of continuous variables and x5 to x7 are binary variables.
Call:
glm(formula = y ~ x1 + x2 + x3 + x4 + x5 +
x6 + x7, family = binomial(), data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.6604 -0.5712 0.4691 0.6242 2.4095
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.84633 0.31609 -9.005 < 2e-16 ***
x1 0.14196 0.04828 2.940 0.00328 **
x2 4.05937 0.22702 17.881 < 2e-16 ***
x3 -0.83492 0.08330 -10.023 < 2e-16 ***
x4 0.05679 0.02109 2.693 0.00709 **
x5 0.08741 0.18955 0.461 0.64467
x6 -2.21632 0.53202 -4.166 3.1e-05 ***
x7 0.25282 0.15716 1.609 0.10769
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1749.5 on 1329 degrees of freedom
Residual deviance: 1110.5 on 1322 degrees of freedom
AIC: 1126.5
Number of Fisher Scoring iterations: 5
The output of the GLM shows that most of my variables are significant for my model, but the various goodness of fit test I have done:
anova <- anova(model, test = "Chisq") # Anova
1 - pchisq(sum(anova$Deviance, na.rm = TRUE),df = 7) # Null Model vs Most Complex Model
1 - pchisq(model$null.deviance - model$deviance,
df = (model$df.null - model$df.residual )) # Null Deviance - Residual Deviance ~ X^2
hoslem.test(model$y, model$fitted.values, g = 8) # Homer Lemeshow test
pR2(model) # Pseudo-R^2
tell me that there is a lack of evidence to support my model.
More over, I have a bimodal deviance plot. I suspect the bimodal distribution is caused by the sparsity of my binary variables.
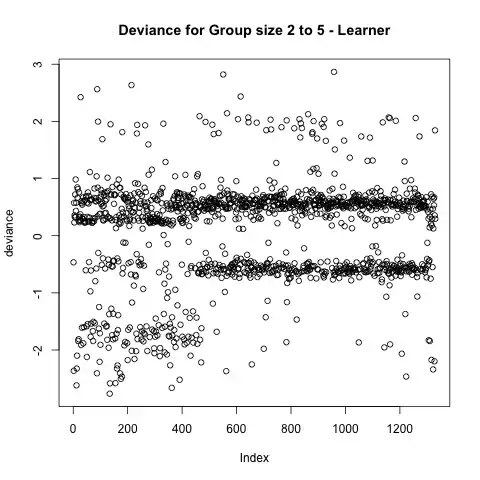
So I calculated the absolute error abs(y - y_hat), and obtained the following:
- 77% of my absolute errors were in [0;0.25], which I think is very good!
On the following plot, Y=1 is red, and Y=0 is green. This model is better at predicting when Y will be 1 than 0.
My question is thus the following:
The goodness of fit tests all assume that my null hypothesis follows a Chi square distribution of some sort. Is it correct to conclude that based on my absolute error, my model's prediction is OK, it's just that it doesn't follow a Chi square distribution and thus perform poorly with these tests?
