4

I have been having trouble with the predict function underestimating (or overestimating) the predictions from an lmer model with some polynomials. Update: The same trouble happens when I use lm models, i.e. it has nothing to do with mixed models. The example code below is still given with lmer models but one can ignore random effects as far as this question is concerned.

I have scaled data (posted here) that looks like this:

Terr      Date     Year            Age  
T.092     123      0.548425     -0.86392            
T.104     102      1.2072       -0.48185            
T.104     105      1.075445     -0.86392            
T.104     112      0.94369      -1.24599            
T.040     116     -0.2421        2.192652           
T.040     114     -0.37386       1.810581           
T.040     119     -0.50561       1.428509           
T.040     128      0.15316      -0.09978            
T.040     113      0.021405     -0.48185

I’m trying to determine how Year affects lay date after controlling for Age, with Terr (territory) as a random variable. I usually include polynomials and do model averaging, but whether I use a single model or do model averaging, the predict function gives predictions that are a bit lower or higher than they should be. I realize that the model below would not be a good model for this data, I’m just trying to provide a simplified example.

Below is my code 

library(lme4)
m1 <- lmer(Date ~ (1|Terr) + Year + Age + I(Age^2), data=data)
new.dat <- data.frame(Year = c(-2,-1,0,1),
                  Age=mean(data$Age, na.rm=TRUE))
Predictions=predict(m1, newdata = new.dat, re.form=NA)
pred.l<-cbind(new.dat, Predictions)
pred.l  

      Year          Age Predictions
    1   -2 2.265676e-16    124.4439
    2   -1 2.265676e-16    123.2124
    3    0 2.265676e-16    121.9810
    4    1 2.265676e-16    120.7496

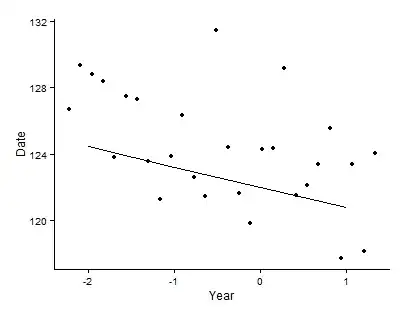
When plotted with the means, the graph looks like this:

graph1

When I use effects, I get a much better fit 

library(effects)
ef.1c=effect(c("Year"), m1, xlevels=list(Year=-2:1))
pred.lc=data.frame(ef.1c)
pred.lc

      Year      fit        se    lower    upper
    1   -2 126.0226 0.6186425 124.8089 127.2363
    2   -1 124.7911 0.4291211 123.9493 125.6330
    3    0 123.5597 0.3298340 122.9126 124.2068
    4    1 122.3283 0.3957970 121.5518 123.1048

graph2

After much trial and error, I have discovered that the problem is with the Age polynomial, because when the Age polynomial is not included, the predicted and fitted are equal and both fit well. Below is the same model but with Age as a linear term. 

m2 <- lmer(Date ~ (1|Terr) + Year + Age, data=data)
new.dat <- data.frame(Year = c(-2,-1,0,1),
                  Age=mean(data$Age, na.rm=TRUE))
Predictionsd=predict(m2, newdata = new.dat, re.form=NA)  
pred.ld<-cbind(new.dat, Predictionsd)
pred.ld

      Year          Age Predictionsd
    1   -2 2.265676e-16     125.9551
    2   -1 2.265676e-16     124.7653
    3    0 2.265676e-16     123.5755
    4    1 2.265676e-16     122.3857

library(effects)
ef.1e=effect(c("Year"), m2, xlevels=list(Year=-2:1))
pred.le=data.frame(ef.1e)
pred.le

      Year      fit        se    lower    upper
    1   -2 125.9551 0.6401008 124.6993 127.2109
    2   -1 124.7653 0.4436129 123.8950 125.6356
    3    0 123.5755 0.3406741 122.9072 124.2439
    4    1 122.3857 0.4093021 121.5827 123.1887

I do many similar analyses, and this issue with the predictions being slightly lower (or higher) than they should be often happens when Age is included as a polynomial. When I include a polynomial for Year, there is no problem and the predicted and fitted are equal, so I know the problem is not with all polynomials.

m3 <- lmer(Date ~ (1|Terr) + Year + I(Year^2) + Age, data=data)

new.dat <- data.frame(Year = c(-2,-1,0,1),
                  Age=mean(data$Age, na.rm=TRUE))
Predictionsf=predict(m3, newdata = new.dat, re.form=NA)  
pred.lf<-cbind(new.dat, Predictionsf)
pred.lf

      Year          Age Predictionsf
    1   -2 2.265676e-16     125.6103
    2   -1 2.265676e-16     124.8494
    3    0 2.265676e-16     123.7483
    4    1 2.265676e-16     122.3070

library(effects)
ef.1g=effect(c("Year"), m3, xlevels=list(Year=-2:1))
pred.lg=data.frame(ef.1g)
pred.lg

      Year      fit        se    lower    upper
    1   -2 125.6103 0.8206625 124.0003 127.2203
    2   -1 124.8494 0.4615719 123.9438 125.7549
    3    0 123.7483 0.4275858 122.9094 124.5871
    4    1 122.3070 0.4262110 121.4708 123.1431

I've looked for answers (e.g., here) but haven't found anything that is directly helpful. Does anyone have any insight?

Community
  • 1
AJ12
  • 66
  • 1
  • 6
  • Does it work correctly if you kick out the random effect and use lm instead of lmer? – amoeba Oct 14 '16 at 20:47
  • 1
    I just ran m1 above without the random effect and using lm instead of lmer, and predict still doesn't work correctly. The predicted values are still a bit lower than you'd expect. Essentially the results of the lm are very similar to what I describe with the lmer, and that matches my experience with other analyses using glm's and glmer's. The presence or absence of the random factor does not appear to make a difference. – AJ12 Oct 14 '16 at 21:12
  • 1
    Your problem has nothing to do with mixed models.

    Your Age is centered to have mean zero. If you only have a linear term + Age in your model, then to get a prediction for each Year you can simply supply Age=0, which is what you are doing in your new.dat dataframe. So it works fine.

     – amoeba Oct 14 '16 at 22:05
  • 1
    But if you have a quadratic term as well, then the combined contribution of Age+Age^2 will not on average be zero, and so your predicted curve will not match to the data. Instead, you need to supply some value $a$ such that $a+a^2$ were equal to the mean of Age+Age^2 in your data. As your Age is standardized, the mean of Age^2 is simply its variance i.e. equals to 1. So you need $a+a^2=1$ which yields $a=0.618$. – amoeba Oct 14 '16 at 22:05
  • @amoeba Thanks but that does not work. When I use Age=0.618 instead of Age=mean(data$Age) or Age=0, the predicted values are even more underestimated. I've been playing with it and the closest predictions are when Age = -0.3216. I can't figure out why though, so it's not that useful. – AJ12 Oct 17 '16 at 20:38
  • 1
    Yes, of course. I did not think about it carefully enough, my apologies. Your model estimates coefficients $\beta_1$ for Age and $\beta_2$ for Age^2. You need to find $a$ such that $$\beta_1 a + \beta_2 a^2 = \Big \langle \beta_1 \text{Age} + \beta_2 \text{Age}^2 \Big \rangle = \Big \langle \beta_2 \text{Age}^2 \Big \rangle = \beta_2 \cdot 1 = \beta_2.$$ So that is the quadratic equation you need to solve. What are the values of these two betas in your model? – amoeba Oct 17 '16 at 22:45
  • 1
    Yes, sorry! I wanted to look at a few things, but here is what I have. For Age it's -4.4009 and for Age^2 it's 1.5800. So -4.4009a + 1.5800a^2 = 1.5800 and one of the solutions for a is -0.32183. Setting Age=-0.32183 does work very well, so thank you. But I will be doing many such analyses with multiple polynomials per model. If people are having to use these solutions from quadratic equations instead of just using a=mean(data$a) to set up their newdata frames when they have polynomial covariates, there must be some example code somewhere? Thanks so much for your help. – AJ12 Oct 18 '16 at 17:45
  • Part of the problem is that I'm not sure I follow the logic for the equation you presented. For example, how would it work if the polynomial were cubic? – AJ12 Oct 18 '16 at 18:28
  • The logic is simple: you want to reproduce the average contribution of all the Age effects in your model. If you had a cubic term, then you would look for $a$ such that $\beta_1 a + \beta_2 a^2 + \beta_3 a^3$ equals the mean of all the Age effects, so it's a cubic equation then. There might be a smarter way to compute that; I don't know. The effects package can handle it, so maybe one can look at how it treats polynomial terms. Can't you simply use the effects package or do you need to compute it manually? – amoeba Oct 18 '16 at 21:53
  • I think this (how to compute such predictions in a simple/efficient way?) could make a great separate question, btw. Perhaps you will want to post it separately. Be sure to get rid of mixed models and formulate everything in terms of lm. It would also be good to have a simple reproducible example - maybe you can include some part of your data. – amoeba Oct 18 '16 at 21:56
  • Yes, effects handles the polynomials very well with a single model, but it doesn't handle model-averaging (using AIC) at all as far as I know. So I have to use predict, which does correctly handle the model-averaging (but not the polynomials, apparently). I will post the question about how to easily compute the predictions if I still can't find the info now that I know what is going on - it just seems like this should be a pretty common problem. Thanks again for your help - glad to know the explanation for this issue. – AJ12 Oct 19 '16 at 14:23
  • I decided that this question is interesting enough to deserve an answer, so I posted one (based on the above comments). Perhaps I could put a bounty or put a link in chat to attract people's attention here. Somebody will surely know what approach effects uses. – amoeba Oct 19 '16 at 14:50
  • That would be very useful. – AJ12 Oct 19 '16 at 15:45

1 Answers1

3

Your problem has nothing to do with mixed models.

Your Age is centered to have mean zero. If you only have a linear term + Age in your model, then to get a prediction for each Year you can simply supply Age=0, which is what you are doing in your new.dat dataframe. And it works fine.

But if you have a quadratic term as well, then the combined contribution of Age+Age^2 will not on average be zero, and so your predicted curve will not match to the data. Instead, you need to supply some value $a$ such that $$\beta_1 a + \beta_2 a^2 = \Big \langle \beta_1 \text{Age} + \beta_2 \text{Age}^2 \Big \rangle = \Big \langle \beta_2 \text{Age}^2 \Big \rangle = \beta_2 \cdot 1 = \beta_2,$$ where $\beta_1$ and $\beta_2$ are the model coefficients for the linear and quadratic Age terms respectively (and I used the fact that Age is standardized, i.e. has zero mean and unit variance). This is a quadratic equation that yields a value of $a$ to put into the dataframe that is passed to predict().

As you wrote in the comments, this does the trick.

This approach can be extended in an obvious way to handle higher-order polynomials, but the equation(s) will get more complicated. I am not sure what strategy the effects package uses to handle it.

amoeba
  • 104,745