I am not able to understand the difference between the joint density function and density function for a random variable $Z = X_1 + X_2$, where $X_1, X_2$ are uniform random variables in $[0,1]$.
I think joint density in this case is $f_{X_1, X_2}\left(x_1,x_2\right) = 1$ (reference)
Likewise the density function $f_Z$ is defined as convolution of $f_{X_1}$ and $f_{X_2}$ (reference: page 8)
Could someone please explain the difference between the two?
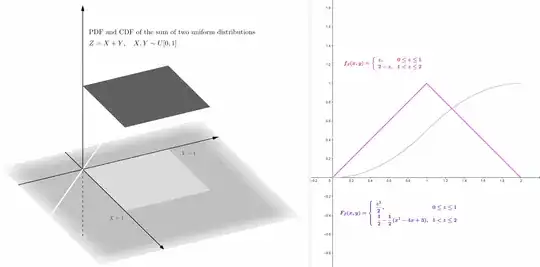
Following up on Glen_b's answer, and in an attempt to dumb it down a bit more, the following illustrations shows how the bivariate or joint pdf of $X$ and $Y$, both independent and standard uniform distributions $U(0,1)$, forms the basis to obtain the pdf of the variable $Z$, defined as the sum of $X + Y.$
For every value of $Z,$ the probability of getting a quantile lower than $Z,$ i.e. the distribution or cdf of $Z$ will be given by the integral from $-\infty$ to the line $z = x + y$ on the $X$ axis, and from $-\infty$ to $+\infty$ on the $Y$ axis. Luckily, the vast majority of the $XY$ plane corresponds to a joint pdf of $0$.
The idea is that by obtaining the cdf, i.e. $F_Z(z)$, of $Z$ we can arrive at the cdf, i.e. $f_Z(z)$, by differentiating:
In general, the pdf of the sum of two independent variables $X$ and $Y$ can be proven to correspond to the convolution of $f_X(z)$ and $f_Y(z)$ at $z$, i.e.
$$f_Z(z)=(f * g)(z)= \int_{-\infty}^{+\infty}f_X(z-y)\,f_Y(y)\,\mathrm dy.$$
Algebraically, the joint density can be expressed by two indicator variables:
$$f_{XY}(x,y)=1\!_{\{(z-y)\,\in\,[0,1]\}}\,1\!_{\{y\,\in\,[0,1]\}}$$
Hence,
$$f_Z(z)=\int_0^z f_{X}(z-y)f_{Y}(y)\,\mathrm dy=\int_0^z 1\!_{\{(z-y)\,\in\, [0,1]\}}\,1\!_{\{(y\,\in\, [0,1]\}}\,\mathrm dy$$
$Z=X+Y$ can reach $2$ inviting the following partition:
and noting that $f_Y(y)=1$ if $0\leq y \leq 1$, and $0$ otherwise,
$$\begin{align} f_Z(z)&=\int_0^1 1\!_{\{(z-y)\in [0,1]\}}\,\mathrm dy\\[2ex] &=\int_0^z \mathrm dy \\[2ex] &= z \end{align}$$
and given that we are integrating over $y$, and the integrand is $1$ only when $0\leq z−y \leq 1$ (rearranged: $z−1\leq y\leq z$):
$$f_Z(z)= \int_{z-1}^{1} \mathrm dy = 2-z$$
explaining the triangular appearance of the $\text{pdf}$ of $Z$.
If you don't write down the support, you may not see what's going on -- but as soon as you do, it's a lot clearer.
I am not able to understand the difference between the joint density function and density function for a random variable Z = x1 + x2 where x1, x2 are uniform rvs in [0,1].
Note that $f_{X_1}(x_1)=1$ for $0<x_1<1$ and $0$ elsewhere; similarly for $X_2$.
The joint density is bivariate - the density is a surface.
I think joint density in this case is f(x1,x2) = 1
So, assuming independence, the joint density will be: $f(x_1,x_2) = f_{X_1}(x_1)\, f_{X_2}(x_2)= 1 \times 1=1$ on the unit square and $0$ elsewhere.
(At least, "bivariate uniform under independence")
Likewise the density function of z is defined as convolution of x1 and x2
It is the convolution if they're independent, yes.
The sum of a pair of quantities is a single quantity -- the sum of a pair of random variables is a univariate random variable.
The density function of the sum of independent variables goes from the sum of the smallest values of each variable to the sum of the largest values of each variable. Consequently the sum of a pair of independent variates each on $(0,1)$ will lie in the interval $(0+0,1+1)$ (i.e. on $(0,2)$).
The shape of the density for the sum (as you'll find if you perform the convolution) is symmetric and triangular, though it's also obvious from direct inspection of a picture of the joint density:
The blue arrows show all the density at a fixed $x_1+x_2$; this is evaluated at each point along the red line. You can see the amount of density at each point increases linearly until the peak at 1, then decreases linearly again.
