7

is there a general solution to that? I have seen simple examples for Y+X=Z but I was wondering how this would be with rescaling?

guest99921
  • 71

2 Answers2

13

If we have a variable $X\sim U(0,1)$ and multiply it by $a$, then $aX\sim U(0,a)$.

Assume that we're dealing with independent continuous uniform on $(0,a)$ and $(0,b)$ respectively (with $a<b$)

(This assumption is not restrictive since we can obtain the general case from this easily.)

Then the joint density is $\frac{1}{ab} I_{(0,a)}\times I_{(0,b)}$.

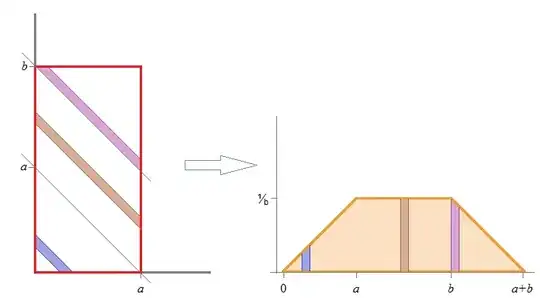
Since the bivariate density is constant where it's non-zero, we can just draw it "looking from above" by marking the boundary of that non-zero region.

Bivariate uniform and corresponding convolution

... and so by elementary geometric argument (along the lines of (i) recognize that density increases linearly as the sum, $z$ goes from $0$ to $a$, stays constant until $b$ and then decreases linearly to $a+b$, and (ii) that the height in the middle section must be $1/b$ to get unit area, then (iii) the equations of the three non-zero sections follow immediately by inspection), the density of the convolution is

$f(z) = \begin{cases} 0 & z\leq 0\\ z/ab & 0<z<a \\ 1/b & a\leq z<b \\ (a+b-z)/ab & b\leq z<a+b \\ 0 & z\geq a+b \end{cases}$

[While formal integration will obviously work, it's somewhat quicker - for me at least - to proceed by something like the above reasoning, where one simply draws the density and then writes the result down immediately.]

The general case:

Imagine instead we had independent $U(c,a+c)$ and $U(d,d+b)$. Then the above density would simply be shifted right by $c+d$.

Glen_b
  • 282,281
  • 1
    Great complement to this other post. The intuition is also clear, as you see the triangle expand from $U(0,1)$. I wish you did elaborate a bit more on the "elementary" geometric argument, though... – Antoni Parellada Aug 05 '16 at 19:42
  • @Antoni that argument goes along the lines of 1. recognize that density increases linearly as z goes from 0 to a, stays constant until b and then decreases linearly to a+b. 2. that the height in the middle section must be 1/b to get unit area (though you can see it other ways as well). 3. the equations of the three non-zero sections follow immediately by inspection. Do you think that would help? (I worried it might be too obvious.) – Glen_b Aug 07 '16 at 02:07
  • 1
    It's perfect. Actually I did become clear after I went through the exercise of putting together the more basic standard uniform videoclip on the post you commented on before (thank you). The color stripes are great. This is a very intuitive topic with some heavy lifting in the background. There is a good youtube on the topic here if someone is interested. – Antoni Parellada Aug 07 '16 at 02:47
6

Define $Y'=aY$ and $X'=bX$, find their distribution, and you are back to the problem you know how to solve: $Y'+X'=Z$ (convolution).

Tea
  • 61
  • Yes, but the convolution result is not the same as the one obtained for the convolution of iid $U(0,1)$ or $U(0,\alpha)$ random variables and requires more work to determine. – Dilip Sarwate Aug 05 '16 at 15:22