How to count near duplicates in a mixed pool using AnyDice?

Question

Following on from this question: How to count duplicates in a mixed pool using AnyDice?

I'm also interested in the much harder question of using AnyDice to look at how much easier some dice mitigation of +/-1 makes getting duplicates (as per the example in that question).

For example, if I rolled 12, 12, 5, 4, 3, 1 the result of how many dice there are that are 1 away from a duplicate would be 3; because 5, 4 and 3 are all 1 away from another result.

Answer 1

The programs given in my answer to your previous question can be fairly easily modified to also count "near misses". Taking advantage of the fact that the input arrays are sorted (in descending order by AnyDice, in ascending order by Python), we can replace the equality comparisons with checks that the difference of adjacent elements is at most 1.

For example, in AnyDice:

function: near dupes in A:s B:s C:s {
  DICE: {A, B, C}
  DUPES: 0
  loop DIE over DICE {
    SAME: [count DIE in DICE]
    NEAR: [count {DIE-1, DIE+1} in DICE]
    if SAME > 1 | NEAR > 0 { DUPES: DUPES + 1 }
  }
  result: DUPES
}
output [near dupes in 1d12 2d10 1d8]

or, if you need a solution less likely to time out for large dice pools, in Python using the dice rolling framework from this answer:

from collections import defaultdict, Counter
summary = defaultdict(float)
for d12, p12 in dice_roll(12, count=3):
  for d10, p10 in dice_roll(10, count=2):
    for d8, p8 in dice_roll(8, count=1):
      prob = p12 * p10 * p8
      roll = Counter(d12 + d10 + d8)
      dupes = 0
      for die, same in roll.items():
        near = roll[die-1] + roll[die+1]
        if same > 1 or near > 0: dupes += same
      summary[dupes] += prob
for dupes, prob in sorted(summary.items()):
  print("%d (near) duplicates: %.2f%%" % (dupes, 100 * prob))

---

Both of the programs above count all dice that either match another die exactly or with a difference of one, but this can be easily changed just by changing one line.

For example, if you wanted to ignore exact matches and only count dice that are ±1 pip away from another die, you could change the condition if SAME > 1 | NEAR > 0 in the AnyDice code to just if NEAR > 0.

Alternatively, if you want to only count dice that are ±1 pip away from another die and don't exactly match any other die, you can instead use the condition if SAME = 1 & NEAR > 0.

In the Python code, you can accomplish the same thing by changing the condition if same > 1 or near > 0 either to if near > 0 or to if same == 1 and near > 0.

(Of course, you can also count only exact matches by changing the condition to just if SAME > 1 in the AnyDice code, or to if same > 1 in Python.)

---

Ps. Note that, in general, the number of "near misses" (whether excluding or including rolls that are also exact duplicates) will not be independent of the number of exact duplicates, so you can't just add them together and get a meaningful result. (Well, you can meaningfully add the averages together due to the linearity of expectations, but that's about all.)

Instead, if you want a detailed view of how including near misses will affect the distribution of the results, compared to not including them, I'd recommend either:

• just plotting the distributions of the number of duplicates with and without near misses and comparing them, e.g. like this (using AnyDice in "at least" graphing mode, for 1d12 + 2d10 + 1d8):

  

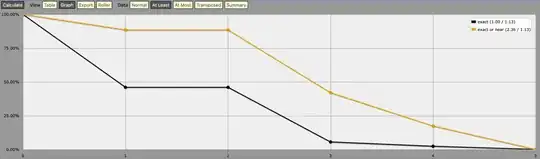
  ^{(Note: The one-in-10-billion "fuzz die" in the linked code above is there to work around what I'd consider a glitch in AnyDice's graph plotting. You can remove it and see how janky the graphs become due to missing values.)}

• or printing a full table of probabilities for all combinations of exact values and near misses, like this (using Python, for 3d12 + 2d10 + 1d8):

  Near misses:	0	1	2	3	4	5	6
  0 exact dupes:	0.15%	—	2.10%	3.09%	6.92%	6.07%	2.67%
  1 exact dupes:	—	—	—	—	—	—	—
  2 exact dupes:	2.92%	6.30%	15.50%	15.35%	7.19%	—	—
  3 exact dupes:	1.95%	2.22%	3.16%	1.22%	—	—	—
  4 exact dupes:	6.23%	8.02%	5.09%	—	—	—	—
  5 exact dupes:	1.98%	1.03%	—	—	—	—	—
  6 exact dupes:	0.85%	—	—	—	—	—	—

  …which you can then analyze and mangle as you want e.g. in a spreadsheet.