I'm looking for a formula to calculate the chance that (n) rolls of a d(y) produces any of (x) specific numbers (k) times, where x,y,n,k > 0, k <= n, and x <= y.
AnyDice is a neat thing to know about, but I'd much rather have the formula itself.
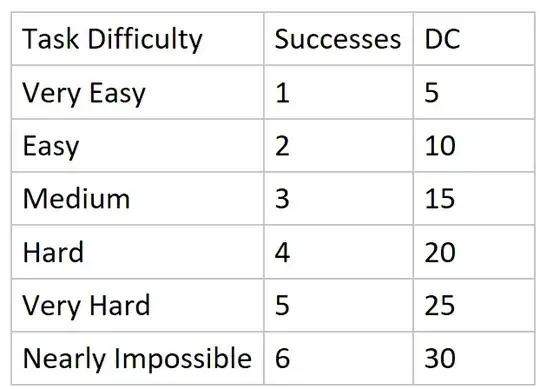
I know this sounds like stat homework but I guarantee you it's for tabletop shenanigans. I recently ran a one-shot combining Hack The Planet, the one page 90's hacker rpg created by Grant Howitt, and D&D 5e, to create a sort of... Persona'esc experience. I created this table:
...to handle contesting rolls between the system. It worked well enough for a one shot but it seemed rolls with 5e's d20 system generally had a leg up over hack the planet's d6's. I'm asking for this formula in order to assist in better balancing any other hackbrained one-shot ideas I think up in the future.