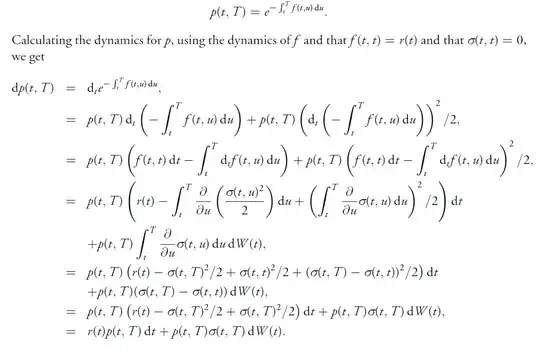I am given the following forward rate dynamics $df(t,u)=\frac{\partial}{\partial u}(\frac{\sigma^2}{2})dt-\frac{\partial}{\partial u}\sigma dW$ and want to calculate the dynamics of the ZCB $p$ via the computations below. The second equality is clearly Ito lemma but equality three and four throws me off completely, can someone see whats going on?
1 Answers
The notations in the snapshot are pretty messy. I prefer to proceed as follows.
Let $X_t = -\int_t^T f(t, u)du$. Note that \begin{align*} f(t, u) - f(0, u) = \frac{\partial }{\partial u}\left(\int_0^t \frac{\sigma^2(s, u)}{2} ds - \int_0^t \sigma(s, u) d W_s \right). \end{align*} Then \begin{align*} r_t = f(t, t) = f(0, t) + \frac{\partial }{\partial u}\left(\int_0^t \frac{\sigma^2(s, u)}{2} ds - \int_0^t \sigma(s, u) d W_s \right)\Big|_{u=t}. \end{align*} Moreover, \begin{align*} \int_t^T f(t, u)du - \int_t^T f(0, u)du &= \left(\int_0^t \frac{\sigma^2(s, T)}{2} ds - \int_0^t \sigma(s, T) d W_s \right) \\ &\qquad -\left(\int_0^t \frac{\sigma^2(s, t)}{2} ds - \int_0^t \sigma(s, t) d W_s \right). \end{align*} That is, \begin{align*} X_t &= - \int_t^T f(0, u)du + \left(\int_0^t \frac{\sigma^2(s, t)}{2} ds - \int_0^t \sigma(s, t) d W_s \right) \\ &\qquad\qquad\qquad\qquad - \left(\int_0^t \frac{\sigma^2(s, T)}{2} ds - \int_0^t \sigma(s, T) d W_s \right). \end{align*} Consequently, \begin{align*} dX_t &= f(0, t) dt + \frac{\sigma^2(t, t)}{2} dt - \sigma(t, t) d W_t \\ &\qquad + \frac{\partial }{\partial u}\left(\int_0^t \frac{\sigma^2(s, u)}{2} ds - \int_0^t \sigma(s, u) d W_s \right)\Big|_{u=t} dt -\frac{\sigma^2(t, T)}{2} dt + \sigma(t, T) d W_t\\ &= r_t dt -\frac{\sigma^2(t, T)}{2} dt + \sigma(t, T) d W_t. \end{align*} Therefore, \begin{align*} dP(t, T) &= d\big(e^{X_t} \big)\\ &=P(t, T)\Big(dX_t + \frac{1}{2} d\langle X, X\rangle_t \Big)\\ &=P(t, T)\big(r_t dt + \sigma(t, T) d W_t \big). \end{align*}
- 21,114
- 1
- 35
- 80
-
I dont quite understand the first equality for $dX$ where does then $\frac{\partial}{\partial u}$-term come from? – user123124 Oct 31 '19 at 18:03
-
Look at the second term $\left(\int_0^t \frac{\sigma^2(s, t)}{2} ds - \int_0^t \sigma(s, t) d W_s \right)$ in $X_t$, there is one $t$ in the integral limit and another $t$ in the integrand. The differential $\frac{\partial}{\partial u}$, and evaluated at $t$, is for the $t$ in the integrand. – Gordon Oct 31 '19 at 18:09
-
right, thats kind of odd.., how do you interpret that, some kind of chain rule? – user123124 Oct 31 '19 at 18:15
-
You need to check the calculus book. How do you calculate the differential $\frac{d}{dx}\left(\int_{a(x)}^{b(x)} g(x, y) dy\right)$? – Gordon Oct 31 '19 at 18:24