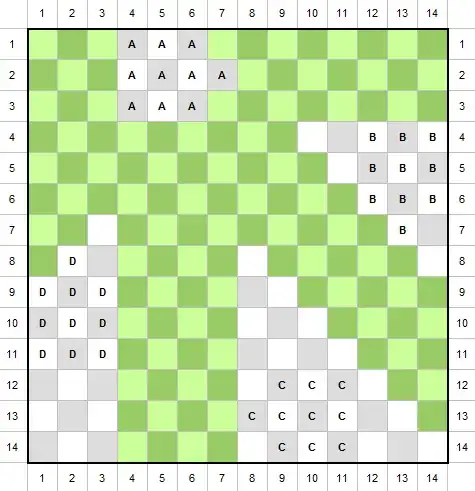
Here's a variation of Discrete Peaceful Encampments: Player 3 has entered the game! (which itself is a variation of Peaceful Encampments).
You have 3 white queens, 3 black queens, 3 red queens, and 3 green queens. Place all these pieces onto a normal 8x8 chessboard in such a way that no queen threatens a queen of a different color.
Okay, that was easier than the previous variations, right? You can probably use the pattern you found to solve these problems as well:
Place 5 queens of each of four different colors onto a 10x10 checkerboard so that no queen threatens a queen of a different color.
Place 7 queens of each of four different colors onto a 12x12 checkerboard so that no queen threatens a queen of a different color.
Which leads to the real puzzle:
At what point does it become possible to place more than $N-5$ queens of each of four different colors peacefully onto an $N\times N$ checkerboard?