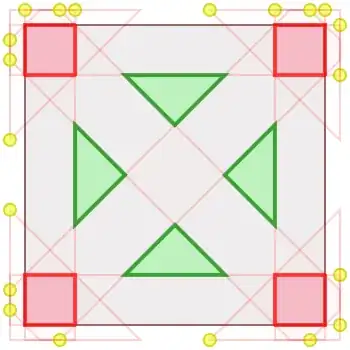
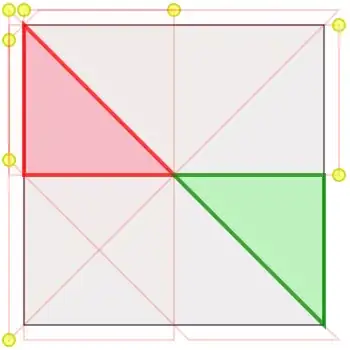
This math puzzle is due to Donald Knuth (as far as I know; maybe he got it from someone else) circa 2014.
Consider a plain represented by the unit square. On this plain we want to “peacefully encamp” two armies of point-sized soldiers — one army red and one army green. Each soldier “attacks” chess-queen-wise: horizontally, vertically, and diagonally in all directions. The puzzle is to maximize the size of the equal armies (equivalently, maximize the size of the smallest army), given the constraint that no pair of opposing soldiers can be placed attacking each other.
(No Cantor sets or anything, okay? Just normal polygons.)
I have a conjectured answer but I don't know if it's really the optimum. If this would be more on-topic for math.SE or something, please comment and let me know!
I have written a little Javascript program to help visualize solutions. You can find it here.
Here are two examples of ways to peacefully encamp armies of sub-maximum size. The total size of each army in the first solution is 1/9; the total size of each army in the second solution is 1/8.
Once you’ve solved that, the next puzzle is to peacefully encamp three armies, four armies, etc... all the way to infinity.
My own candidate solutions have army size $\frac{7}{48} \approx 0.1458$ (for 2 armies), $\sim 0.0718$ (for 3 armies), $0.05$ (for 4 armies), and $\sim 0.0311$ (for 5 armies).