8

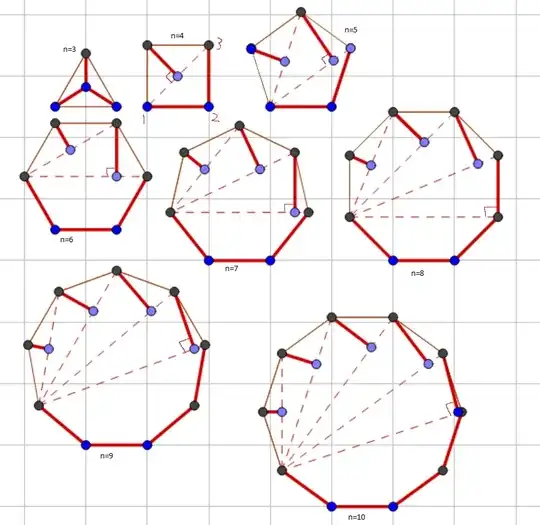
You have the same plugging task as in Find a straight tunnel , but now the problem requires a bit more imagination:

Bob has a field, which is a regular polygon with $N$ sides and perimeter $P$. There is a tunnel, which is just under the surface, but invisible - unless you dig. It is known that the tunnel goes under the field (at least touches it at one point), it is straight and infinitely long (in both directions).
Bob wants to find the tunnel. To do this he has a plow and can dig along some lines with it. If Bob plows and crosses the tunnel he will find it. Bob doesn't want to plow too much so he first figured a strategy out, which guarantees to find the tunnel by plowing at most $L$ meters.
What can be the smallest $k = L/P$ ratio, given $N$ can be any number from 3 to $\infty$?
Bob is allowed to plow only inside of his field. He can take the plow out of the ground and move it over the ground without plowing.

Important to note that now you can plow only inside and you can chose the field, which is best for you (i mean to chose $N$).

I tried extreme cases:
$N=\infty$ - it is circle and the best path is along the perimeter, so $k_{min}=1$.
$N=3$ - it is triangle, I belive the best case is a path along medians, then $k_{min}=1/\sqrt{3} \approx 0.5774$.
The best case should be somewhere inbetween.

Community
  • 1
klm123
  • 16,216
  • 8
  • 64
  • 125
  • @Oray, I will recheck my 0.5701 result, but are you sure this theory was talkingabout L/P, not something else? – klm123 Dec 29 '16 at 20:20
  • It seems that for N=3 you have 2/3 in worst case - assuming the tunnel touches a corner. What is the strategy that guarantees the value you derived? – Moti Dec 30 '16 at 05:09
  • @Moti, "path along medians". 3/sqrt(3) is 2/3 of the all medians in the triangle. – klm123 Dec 30 '16 at 07:35
  • I see now. Was this proved? So why not extend it to other cases? – Moti Dec 30 '16 at 17:45
  • For N greater than 5 it will be (N-1)/N (will check for 5 and 4) – Moti Dec 30 '16 at 20:04
  • Are '0 length digs' allowed? – DrunkWolf Dec 31 '16 at 18:16
  • For $N=\infty$ why is the best path the circumference? Hasn't it been proven on the previous question that a better path exists? – greenturtle3141 Jan 02 '17 at 06:33
  • The tunnel could tangentially touch a circle at any point on the circumference, therefore every point on the circumference must be plowed to guarantee finding the tunnel. And once you've done that, anything else is redundant. – Neil W Jan 02 '17 at 06:47
  • @DrunkWolf, let's say yes, but I don't think this will help anywhere. – klm123 Jan 02 '17 at 20:13

3 Answers3

4

This seems a little tricky to prove...

I hope the attached image explains my optimisation for the first n-sided polygon. I'll try to explain step by step.

First, n=3 is the exception and the best route is the path along the medians. Consider the case where n>3:

Begin with one vertex labelled (1). Trace the perimeter to the next vertex(V). Keep tracing to the next vertex until you find a vertex whereby (1),(V), and (V+1) forms an acute triangle. This allows you to drop an altitude from vertex(V+1) onto the line (1)-(V). From then on, repeat the same process for every vertex henceforth.

For the case of a square, we trace out the perimeter until the 3rd vertex, whereby it is more "economical" to drop the altitude to the line (1)-(3) than to trace out the next side. This shape will fully cover any possible tunnel going through the shape.

Let's take n=9 as another example. We can trace out four sides (or 5 vertices) until we see that the next vertex (6) would allow us to drop the altitude to line (1)-(5). Then, we repeat for every subsequent vertex that follows.

This is more economical than the naive solution of tracing out the entire parameter for each shape. I don't have a mathematically rigorous proof that these are the minimum cases for how much we need to plough, and hope the images can intuitively present that it may be the optimum solution.

Ultimately, this appears to give the minimum case that N=3 is the lowest L/P ratio. N=4 gives a L/p ratio of roughly 0.677, and the ratio slowly increases as n increases until we reach the limit of a circle, whereby L/P=1.enter image description here

skyeriding
  • 71
  • 4
  • good job for big N's! I didn't know this solution. But for square and pentagon, at least, you can do better with other strategy. – klm123 Jan 02 '17 at 18:12
  • @klm123 The two solutions for the square I considered were either making an "X" that crosses the centre of square (this gives plough length of $2\sqrt 2$) versus the solution I propose which is $2+\frac{\sqrt 2}{2}$, which is the smallest value I could find. Or am I incorrect and there is yet another solution for the square I haven't considered? My other guess would likely then be an angled "H" shape at 30deg...but I calculated it as $1+\frac{3}{\sqrt 3}$ which is still higher than the above. – skyeriding Jan 02 '17 at 18:29
  • for N=4 you can do at least 0.660 – klm123 Jan 02 '17 at 22:19
  • @skyeriding For n=4, instead of drawing a perimeter between 123, treat it as an irregular n=3. I'm showing this as approx. 0.6597. Similar optimizations may be possible for the perimeters on your higher n. – dmitch Jan 04 '17 at 17:56
2

(Not a complete answer - total hypothesis, without mathematical backing or final calculation, but I believe it's correct)

We can't dig outside of the polygon. Therefore, in order to account for cases where the tunnel goes touches a corner of the polygon, our digging map must include all corners of the polygon.

If we dig a network that connects all the corners of the polygon, it's easy to see that we ensure we'll be able to find any tunnel that passes THROUGH the polygon (a tunnel passing through the polygon will have at least a vertex on either side, and our network of digging connects those vertices, therefore our network intersects the tunnel).

Now, the optimal network for joining points is actually quite obscure. I remember the solution (the network should consist of digging straights that intersect at 120 degrees only), but a 2 minute google search didn't give me a mathematical calculation nor an easy way to generally generate such a network. However, check out https://www.unige.ch/~gander/Preprints/BDM56-GanderE.pdf which should give you a general idea of the point I'm trying to convey.

TheGreatEscaper
  • 11,946
  • 1
  • 42
  • 96
  • The thing is - we don't Have to connect all corners. Most probably the best solution won't do it. – klm123 Jan 02 '17 at 07:04
0

The ratio (N-1)/N is for N>4. For 3, 4 go through the center from vertices N times. For 5 and up go through N-1 edges.

Moti
  • 2,239
  • 10
  • 21