Blindfolded and disoriented near a space station

Question

Following on from the recent blindfolded near the great Wall of China puzzle.

Suppose you are floating in space a mile away from a huge space station (the death star perhaps). Assume that the death star is essentially an infinite plane, and you want to get to it. The only way is to bump into it. But it could be in any direction. What's the shortest distance you could fly in your space suit to guarantee you'll hit it? Assume there's no gravity or other sensors available.

Are we going to get blindfolded in hyperspace 1 mile in the fourth dimension from our plane of existence next? — MPeti, Jan 24 '16 at 13:57
One should note that the problem is equivalent to "What is the shortest path in $\mathbb R^3$ starting at the origin whose convex hull contains the sphere?" - which is analogous to a statement used in a paper linked from the previous question. — Milo Brandt, Jan 24 '16 at 19:11
@MPeti I thought this was simply a trivial extension of the Great Wall puzzle, but there is one important difference: a point can traverse the circumference of a circle in a finite distance, but it can't traverse all points on the surface of a sphere in a finite distance. — Lawrence, Jan 26 '16 at 06:40
Are we guaranteed that our space suit will keep us alive long enough and that it allows precise navigation, or should we all just curl up in a ball against the utter despair of floating off into the infinite emptiness of outer space? — Ian MacDonald, Jan 26 '16 at 14:15
I actually posted this problem on math.stackexchange.com here. In the comments I describe a path of length $13.912\ldots$. — dshin, Jan 31 '16 at 16:44
Infinite plane, zero gravity, no air resistance - now all we need is a frictionless pulley and this is a bona fide high school physics problem. — Akshat Mahajan, Feb 13 '19 at 16:52

score 8 · Accepted Answer · edited Apr 13 '17 at 12:50

8

A simple upper bound is $\sqrt{2} + 2\times 2\pi + 2 \approx 15.98$ miles.

If we travel on two circles of radius $1$, parallel to each other and $2$ miles apart, and whose centers are collinear with the starting point, we can guarantee to hit the space station. To do this, we travel $\sqrt{2}$ miles to the circumference of the first circle, travel around it, then travel the $2$ miles to the other circle and travel around that.

As @MPeti mentioned in the comments below, we can improve this by using the optimal path in the 2-d version instead of circles. The length of the path now becomes $\sqrt{2+\frac{1}{3}} + 2\times(\frac{7\pi}{6}+1+\sqrt{\frac{4}{3}-1}) + 2 \approx 14.01$ miles.

If we don't travel the last mile in the 2-d path and travel between the two paths in a triangular fashion, and realise that the optimum path in 2-d is not necessarily the optimum path in 3-d, we can reduce the length further to approximately $12.74$ miles.

A graphic to help visualisation (made using GeoGebra):

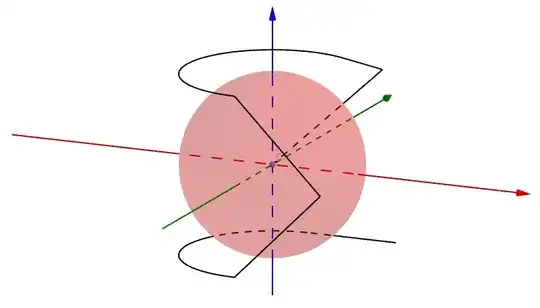
The length of the top path + the initial radial path is $\frac{3\pi}{2}-\theta+\tan{\frac{\theta}{2}}+\sqrt{\sec^2{\frac{\theta}{2}}+1}$, which according to Wolfram Alpha is minimised when $\theta \approx 1.14372$ with a length of $l_1 \approx 5.76604$ miles.

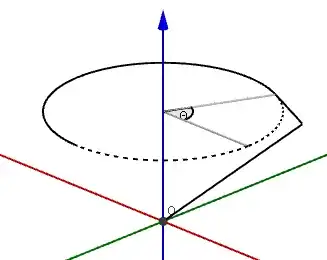
The length of the bottom path is $\frac{3\pi}{2}-\theta+\tan{\frac{\theta}{2}}$, which is minimised when $\theta = \frac{\pi}{2}$ with a length of $l_2 = \pi + 1 \approx 4.14159$ miles.

Adding these two lengths and the length of the semicircular path between them, we arrive at a total length of $l_1 + 2\sqrt{2} + l_2 \approx 12.74$ miles.

edited Apr 13 '17 at 12:50

Community

1

answered Jan 24 '16 at 07:20

Volatility

5,099
1
21
42

You could improve this by taking the top solution to the Wall of China puzzle and tracing that shape instead of circles, I think. That would make the result 2*(1+√3+7π/6) + 2 = 14.79 miles. – MPeti Jan 24 '16 at 13:23
(That calculation is wrong, but you get the idea. Got to stop procrastinating, so not fixing it right now. :) ) – MPeti Jan 24 '16 at 16:43
@mpeti, you need the initial radial path outwards too, I think – Dr Xorile Jan 24 '16 at 18:10
Yes, but another mistake was including the old radial part twice. Correctly, it's [the radial path] + 2around + 2 = √(7/3) + 2(7π/6 + 1) + 2 = √(7/3) + 7π/3 + 4 = 12.86 miles. – MPeti Jan 24 '16 at 18:37
1

By my calculation this path is a little over 14.01. There's a straight segment that you're still missing in the two paths – Dr Xorile Jan 24 '16 at 21:07
I should have added that I have a lower answer than this... – Dr Xorile Jan 25 '16 at 01:20
Nice graphs though? What software are you using? – Dr Xorile Jan 25 '16 at 01:21
It looks like you could get away with "tightening" the vertical semicircle, though I have no idea how much exactly... – MPeti Jan 25 '16 at 09:04
It's difficult for me to verify this. Can you give a list of the co-ordinates of the key points (where it switches from one shape to another). It looks like an excellent solution – Dr Xorile Jan 26 '16 at 16:59
What I'm concerned about is whether the sphere pokes through the triangle formed by the first point reached and the first of the lines moving between the layers; and the triangle formed between the final point reached and the second of the lines moving between the layers. – Dr Xorile Jan 26 '16 at 20:16
@DrXorile first point: (1, 0.6436, 1); points of lines moving between layers: (0, -1, 1), (1, -1, 0), (0, -1, -1); final point (1, 1, -1). I believe the second triangle is tangential to the sphere, and the first completely misses it. – Volatility Jan 27 '16 at 06:24
@DrXorile the plane through the three points should be x-0.6084y+z=1.6084, and the distance from the origin should be around 1.0447, if I'm not mistaken. – Volatility Jan 29 '16 at 05:56
Sorry, I took a while to do this. You're correct in your distance from the origin. It suggests that there are a few tweaks that could reduce the distance further, but I think the broad concept is pretty good! – Dr Xorile Feb 18 '16 at 23:25

Blindfolded and disoriented near a space station

1 Answers1

Linked