I want to formulate a game of darts as a dynamic program again. This question is closely related to my previous post where I wanted to minimize the number of throws to reach checkout. Now the goal is to minimize the number of turns.
A turn consists of three darts. Each dart is used unless you win by checkout, or go bust in which case you revert to the score before the turn started. A state can be described as (s, i, u) where
- s is the score at the beginning of the turn
- i ∈ {1, 2, 3} is the number of throws remaining in the turn
- u is the score within the turn
In addition, we have z that represents the outcome of the dart throw.
z ∈ {Miss, S1, S2, S3, ..., D1, D2, D3, ..., T1, T2, T3, SB, DB}
Each z represents a numerical score. For example, h(T20) = 60. We assume that a player can aim at sixty specified points on the dartboard. The aiming location is defined as µ. If µ = D1 then the player aims at the center point of the D1 region. However, when the player aims at D1, there is also a possibility that the dart ends up in the S1. This probability is defined as p(S1; D1). Logically, each throw results in a value for z. Hence,
If i = 3, there are three darts to be throwed. Hence u = 0. The state transition now satisfies (s*, i*, u*) = f((s, i, u), z) where
The Bellman equation is defined as:
With V(0,i,u) :=0 for any i, u. A turn is counted only when the turn has been completed. This is the case when there is a checkout, bust or the third dart is thrown. There is a monotonic structure so we can solve the recursively by considering states in increasing order like V(2,i,u), V(3,i,u), …, V(501,i ,u). All of the above can be found on page 13 and 14 of the following paper.
Let’s say that s = 2. If s = 2, u is always equal to 0, otherwise there would be a bust. Do we start with calculating V(2,3,0) or V(2,1,0)? So, do we solve the states in increasing or decreasing order of i?
V(2,3,0) I believe there are three possibilities:
- checkout; throw z = D1 -> V(0,3,0)
- miss; throw z = miss -> V(2,2,0)
- bust; throw anything other than D1 and miss -> V(2,3,0)
If we insert this in the Bellman equation, we get the following:
V(2,3,0) = [1 + V(0,3,0)] p(D1;µ) + [0 + V(2,2,0)] p(miss;µ) + [1 + V(2,3,0)] (1 – p(D1;µ) – p(miss;µ))
V(2,3,0) = p(D1;µ) + p(miss;µ)V(2,2,0) + 1 – p(D1;µ) – p(miss;µ) + V(2,3,0) – p(D1;µ)V(2,3,0) – p(miss;µ)V(2,3,0)
V(2,3,0) = p(miss;µ)V(2,2,0) + 1 – p(miss;µ) + V(2,3,0) – p(D1;µ)V(2,3,0) – p(miss;µ)V(2,3,0)
V(2,1,0) If we should start with i = 1 then the possible outcomes lead to the following states:
- checkout; throw z = D1 -> V(0,3,0)
- miss; throw z = miss -> V(2,3,0)
- bust; throw anything other than D1 and miss -> V(2,3,0)
Inserting this, gives:
V(2,1,0) = [1 + V(0,3,0)] p(D1;µ) + [1 + V(2,3,0)] (1 – p(D1;µ))
V(2,1,0) = p(D1;µ) + 1 – p(D1;µ) + V(2,3,0) – p(D1;µ)V(2,3,0)
V(2,1,0) + p(D1;µ)V(2,3,0) = 1 + V(2,3,0)
Both value functions have an unknown term. Please show me where I should start / how I save the Bellman equation for s = 2. Thanks
Updated
I calculated V(2,2,0):
V(2,2,0) = [1 + V(0,3,0)] p(D1;µ) + [0 + V(2,1,0)] p(miss;µ) + [1 + V(2,3,0)] (1 – p(D1;µ) – p(miss;µ))
V(2,2,0) = p(D1;µ) + p(miss;µ)V(2,1,0) + 1 – p(D1;µ) – p(miss;µ) + V(2,3,0) – p(D1;µ)V(2,3,0) – p(miss;µ)V(2,3,0)
V(2,2,0) = p(miss;µ)V(2,1,0) + 1– p(miss;µ) + V(2,3,0) – p(D1;µ)V(2,3,0) – p(miss;µ)V(2,3,0)
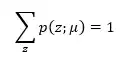
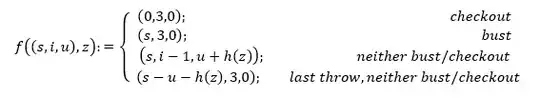
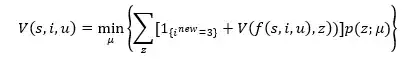
V(2,2,0)has two unknown variables – HJA24 Sep 30 '21 at 14:37