I want to formulate a game of darts as a dynamic program. The goal is to minimize the number of darts thrown while reaching checkout. A dart player has a score s. If his score is s = 2, there is only a single legal / possible move.
- He can checkout by throwing at
D1 - Every other action is not legal and results in a so-called bust and
the score remains the same, s =
2
The above can be formulated as:
where z represents the outcome on the dartboard
z ∈ {S1, S2, S3, ..., D1, D2, D3, ..., T1, T2, T3, SB, DB}
The corresponding numerical scores are h. So if z=T20, h=60
Now the Bellman equation for this DP satisfies:
Where V(s) is the value function when the score is equal to s. In addition, mu is the aiming location on the dartboard. The reward of each action is equal to 1 (because one dart is thrown). In addition, we have p, the probabilities of reaching s_i+1 when aiming at mu, and the corresponding value function of s_i+1. The terminal condition V(0) is equal to 0. All of the above can be found op page 13 here
So, inserting all for s = 2, excluding the illegal moves, leads to the following:
V(2) = min{1 + (V(0) * p(D1;mu))
Lets assume there are two possible values for mu, namely the center of D1 and the center of D19, which is on the opposite of the dartboard. Logically
p(z=D1, mu=center D1) > p(z=D1, mucenter D19)
However, V(0) = 0, so
p(z=D1, mu=center D1) * V(0) = p(z=D1, mu=center D19) * V(0) = 0
So, if we want to minimize the Bellman curve, there is no optimal solution. Both options lead to the same result, V(2) = 1. However, logical reasoning would suggest aiming for mu = center D1 is the optimal / desired solution. What am I doing wrong here?
So, I thought maybe I should add the illegal moves into the Bellman equation. This would look as follows:
V(2) = min{1 + sum((V(0) * p(D1;mu)) + (V(2) * p(S1;mu)) + (V(2) * p(S2;mu)) + ... + (V(2) * p(T19;mu)) + (V(2) * p(T20;mu)))
However, now there is a circular reference for all the illegal moves. How should this be addressed? Should the illegal moves be added? Please help me explain what I am doing wrong.
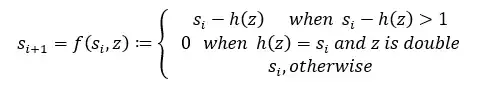
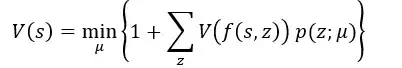
zis {S1, S2, S3, ..., D1, D2, D3, ..., T18, T19, T20}.his the numerical score of z. For exampleh(T20) = 60.pis the probability of throwingzwhen aiming formu.Vis the value function.fis the formula that subtractshfroms.sis the score {0, 1, ..., 501}. – HJA24 Sep 15 '21 at 08:37Vis the value function and represents the value of each score / state – HJA24 Sep 15 '21 at 10:39Vis the expected number of darts thrown. In this case, the recursive formula looks wrong to me. Can you justify it? Maybe it would be easier with $S(v)$ the expected score using $v$ darts – fontanf Sep 15 '21 at 14:11