Exactly as the title suggests
Is there a formula for the future value of monthly payments with annual compounding?
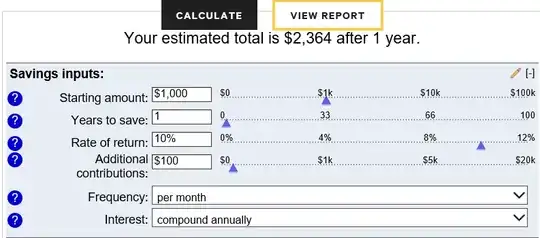
Perhaps approximating the outcome achieved by the following calculator?
https://www.bankrate.com/calculators/savings/compound-savings-calculator-tool.aspx
With frequency set to monthly and compounding set to annually?
Even an approach to interpolating the result would be helpful.
Thank you.
i, you can convert it to the effective monthly rate,m, bym = i/12. Otherwise, for instance ifiis a nominal annual rate compounded quarterly, first convert to an effective annual rate,r, by the formula in this link :r = (1 + i/n)^n - 1. Then you can calculate the monthly rate, or whatever rate is required, bym = (1 + r)^(1/n) - 1. – Chris Degnen Jan 24 '19 at 20:44