-2

This is higher dimension conjecture of Problem 3845 in Crux Mathematicorum and Theorem 2 in here:

PS: This figure is very nice, this is also generalization of Brianchon’s theorem, The Pascal theorem, the Seven circle theorem...etc..... with higher dimension (These are some very nice theorems in plane Geometry). But I don’t know why some one vote down?

I don’t think this question is not good than:

Does this geometry theorem have a name?

The Eyeball Theorem generalized

But the questions above have many vote up. But why some one vote down my question?

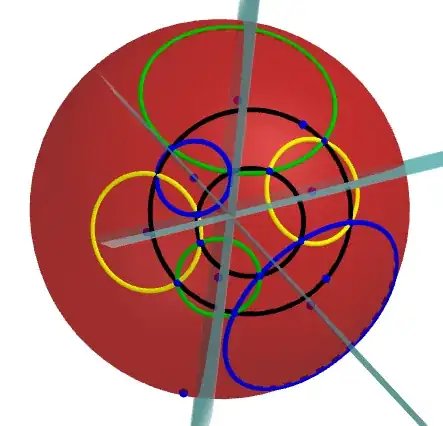
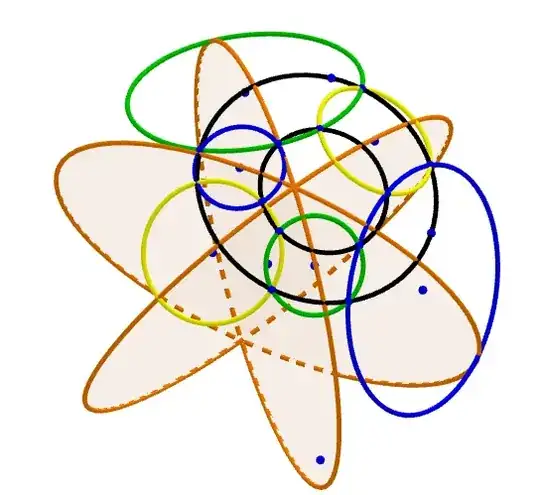
My question: The conjecure as follows true for $2$-sphere. Is the conjecture true for n-sphere $(n>2)$?

Conjecture: Let two circle $(C_1)$, $(C_2)$ on n-sphere $(O)$. Let $1, 2, 3, 4, 5, 6$ be six arbitrary points in $(C_1)$. Let $1'$ be arbitrary point in $(C_2)$. The circle $(121')$ meets $(C_2)$ at point $2'$. The circle $(232')$ meets $(C_2)$ again at $3'$, define points $4', 5', 6'$ similarly. Let $P_1, P_2, \cdots, P_6 $ are the center of circles $i{i+1}{i+1}'i'$ for $i=1, 2, \cdots, 6$. Are three planes $(P_1P_4O)$, $(P_2P_5O)$, $(P_3P_6O)$ share the same line ?

  • Circles $(P_1)=(122'1')$, $(P_4)=(455'4')$ are yellow.

  • Circles $(P_2)=(233'2')$, $(P_5)=(566'5')$ are green.

  • Circles $(P_3)=(344'3')$, $(P_6)=(611'6')$ are blue.

enter image description here

enter image description here

Gerry Myerson
  • 39,024
Đào Thanh Oai
  • 1,086
  • This figure is very nice, this is also Brianchon’s theorem with higher dimension. But I don’t known why some one vote down – Đào Thanh Oai Jul 28 '18 at 15:43
  • I didn't downvote, but I'm guessing people consider your question too elementary for this site. (Whether the picture looks nice doesn't really affect that.) – Jim Conant Jul 28 '18 at 16:03
  • @JimConant I don’t think this question is good but many vote up https://mathoverflow.net/questions/284458/does-this-geometry-theorem-have-a-name – Đào Thanh Oai Jul 28 '18 at 17:18
  • And I don’t thinks this question is good. But many vote up. https://mathoverflow.net/questions/152192/the-eyeball-theorem-generalized – Đào Thanh Oai Jul 28 '18 at 17:22
  • 1
    On the $n$-sphere with $n > 2$, if two circles meet at a point, then they don't necessarily meet at another point. The question seems to be not well-prepared. I vote to close. – Ivan Izmestiev Jul 28 '18 at 18:18
  • @IvanIzmestiev Oh?? With n=2 we can replace 8 circles by 8 planes the result is exactly same. – Đào Thanh Oai Jul 29 '18 at 02:31
  • Please do not vandalize your question, Dao. – Gerry Myerson Jul 30 '18 at 23:50
  • @GerryMyerson This question is not well-come at here. So I want deleted the question. I want send it to AMM – Đào Thanh Oai Jul 31 '18 at 01:59
  • @GerryMyerson This question is very nice with me. There are one hundred corollary, special case of this theorem. So I want deleted this to poist on AMM – Đào Thanh Oai Jul 31 '18 at 02:01
  • You got (and accepted) an answer. Deleting the question is vandalism. Please stop it. – Gerry Myerson Jul 31 '18 at 02:50
  • 3
    Deleting the contents of a question is against site policy. You can delete your question if you have not received an answer with positive net score, but otherwise you can't deface a question. Besides, the person who answered put work into the answer; please have some respect for that, and move on. – Todd Trimble Jul 31 '18 at 03:05

1 Answers1

5

If I correctly understand the construction, everything happens in the $3$-dimensional affine space spanned by the circle $C_1$ and the point $1'$. (In particular, $C_2$ has to lie in this space or the points $2',\dots,6'$ won't exist.) Since everything is also on the surface of an $n$-sphere, we can confine attention to the intersection of the affine $3$-space and the sphere, which is a $2$-sphere. So the general case reduces to the case of the $2$-sphere.

Andreas Blass
  • 72,290
  • 2
    And for the two-sphere it is obvious: they touch the ellipse with foci at centers of circles $(C_1)$ and $(C_2)$. For the proof your just need to check that perpendicular bisectors to $11'$ and $22'$ forms equal angles with $P_1C_1$ and $P_1C_2$. – Arseniy Akopyan Jul 28 '18 at 13:35
  • This figure is very nice, this is also Brianchon’s theorem with higher dimension. But I don’t known why some one vote down – Đào Thanh Oai Jul 28 '18 at 15:43
  • @ArseniyAkopyan Thank You very much for your answer. But can You delete your answer ? Because I don't wan this theorem are not welcome at here. I want delete my question. – Đào Thanh Oai Jul 30 '18 at 06:22
  • @ArseniyAkopyan This question is very nice with me. There are one hundred corollary, special case of this theorem. But this question is not welcome at here. So I want deleted the question to posed on AMM Please help me delete – Đào Thanh Oai Jul 31 '18 at 02:03