The Eyeball Theorem generalized

Question

I have not seen the 2D Eyeball Theorem—that tangents from the centers of two circles, each encompassing the other, intersect each circle in the same segment length—generalized to higher dimensions. It generalizes easily: the radius of the circles of cone/sphere intersections in $\mathbb{R}^3$ (below, red) are equal:
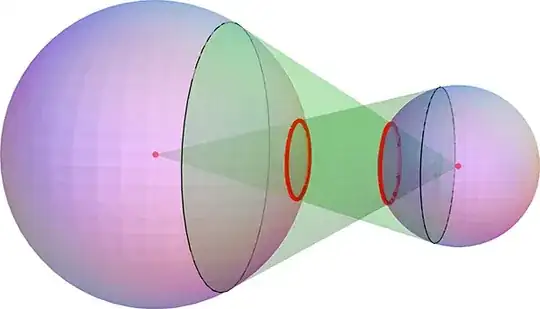
EyeBall
What I am wondering is if there is a sense in which some form of this theorem generalizes to other objects: axis-aligned cubes, ellipsoids, or other shapes. Or does the theorem in some sense characterize spheres? If anyone has seen this addressed previously, I'd appreciate a pointer. Thanks!

(Added). This seems to work for squares/cubes:
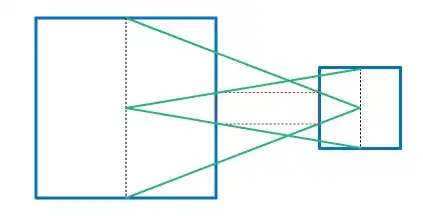
EyeSquare

I think I would have enjoyed this image much more had I not read "eyeball theorem" in the title! — Vidit Nanda, Dec 18 '13 at 01:02
And I would probably not have opened the question without the eyeball reference in the title! That is lovely, the theorem (in the plane) and the image. — Asaf Karagila, Dec 18 '13 at 01:14
Of course this also works for axis-aligned ellipses of the same eccentricity. — Gerardo Arizmendi, Dec 18 '13 at 19:30
One generalization to squares fails. If you consider the lines connecting the centers of the squares to the visible corners of the other square, these don't have the same size "arcs." For example, axis-aligned squares of sides $2$ and $4$ whose centers are distance $10$ apart in the direction of an axis produce arcs of sizes $4/9$ and $1/2$. Your diagram for squares shows secant lines from the centers of squares to the centers of sides, not to the corners that I think would be analogues of tangent lines. — Douglas Zare, Dec 19 '13 at 03:22
@DouglasZare: Yes, my "generalization" for the square only succeeds by changing the tangent to a secant. — Joseph O'Rourke, Dec 19 '13 at 12:00
Unfortunately this doesn't work if we rotate the squares $45$ degrees. — Douglas Zare, Dec 22 '13 at 17:58
Well, for a rotationally symmetric 3D configuration the result is equivalent to the 2D configuration obtained by intersecting with the plane containing the axis, so the quest is for 2D objects, I guess. Did you try Reuleaux triangles? Because of constant diameter it's possible that the theorem would hold regardless of their relative orientation, leading to a non-symmetric configuration. Ditto Reuleaux tetrahedrons. — Michael, Dec 23 '14 at 16:44
Trying to interpolate between circles and squares, I tried with curves of the type $(r^d-x^d)^{1/d}$ but this does not work with the "obvious" generalization. — Per Alexandersson, Dec 23 '14 at 20:13
Dear Dr. @JosephO'Rourke Please help me comment at here: http://mathoverflow.net/questions/250730/a-generalization-of-the-british-flag-theorem-in-euclidean-three-space
Thank to You very much — Oai Thanh Đào, Sep 26 '16 at 10:56
Dear Dr. @Michael Please help me comment at here: http://mathoverflow.net/questions/250730/a-generalization-of-the-british-flag-theorem-in-euclidean-three-space
Thank to You very much — Oai Thanh Đào, Sep 26 '16 at 10:57
My intuition is that this eyeball theorem can be seen as a particular case of the conservation of étendue in geometrical optics, but I haven't been able to see precisely how. — Gro-Tsen, Dec 15 '22 at 14:13

Emmanuel García · Answer 1 · 2014-12-25T18:57:41.713

2

I have introduced some variants of the Eyeball theorem and also seems to admit generalizations in 3D. And as if that were not enough the Archimedean twins have been brought together with these theorems. See link below

http://geometriadominicana.blogspot.com/2014/03/praying-eyes-theorem.html

edited Dec 25 '14 at 18:57

answered Dec 23 '14 at 14:31

Emmanuel García

83
6

And you have posted a related question at http://mathoverflow.net/questions/191719/the-praying-eyes-theorem-generalized – Gerry Myerson Dec 29 '14 at 18:15

The Eyeball Theorem generalized

1 Answers1

Linked