According to one possible definition, an $n$-tangle $T$ is a subset $T \subseteq \Bbb{R}^2\times [0,1] =: X$ that is homeomorphic to a disjoint union $[0,1] \times n := [0,1] \amalg \ldots \amalg [0,1]$ of $n$ copies of the unit interval via an embedding $\iota: [0,1]\times n \hookrightarrow X$ mapping the $2n$ endpoints $\{0,1\}\times n$ onto the $2n$ marked points $\{0,\ldots{},n-1\}\times\{0\}\times \{0,1\}$.
Two tangles $T, T'$ are said to be equivalent, if there is an isotopy $\phi: [0,1] \rightarrow \text{Homeo}(X)$, $\phi(0) = \text{id}$ fixing the boundaries, i.e. such that $\phi(t)(x) = x$ for all $t \in [0,1], x \in \Bbb{R}^2\times \{0,1\}$, such that $\phi(1)(T) = T'$.
There is a remarkable class of $2$-tangles discovered by Conway, the rational tangles which up to equivalence can all be obtained from the trivial $2$-tangle $T = \{0,1\} \times [0,1]$ by an action of $\text{GL}_2(\Bbb{Z})$ on tangle diagrams, described in terms of (redundant) generators as follows:
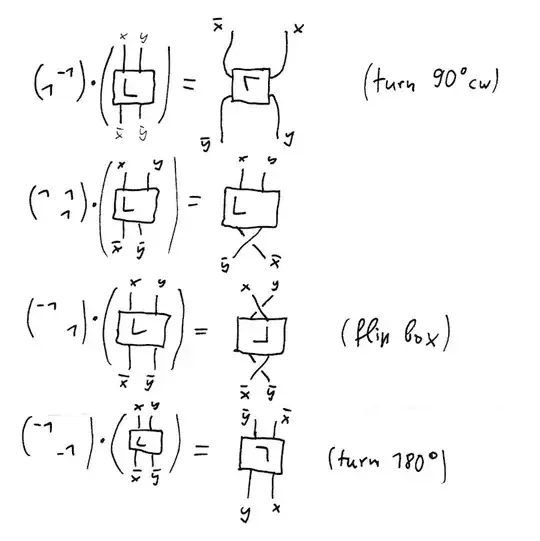
The theory shows that there is a bijection
$$ \frac{\{\text{rational tangles }T\}}{\text{equivalence}} \simeq \Bbb{P}^1(\Bbb{Q}) $$
that's equivariant for the natural actions of $\text{GL}_2(\Bbb{Z})$. In essence, the proof relies on the theory of continued fractions. In particular, to any finite continued fraction expression $$[a_0; a_1,\ldots,a_n](X)$$ defined recursively by $$[](X) := X,\ [a_0; a_1, \ldots, a_n, a_{n+1}](X) := [a_0; a_1, \ldots, a_n](a_{n+1} + X^{-1})$$ one can associate a corresponding rational tangle by formally substituting the trivial tangle for $X$ and expanding this formal fraction using the description of the actions of the generators of $\text{GL}_2(\Bbb{Z})$.
Now, once you accept that rational tangles are basically the same thing as finite continued fractions the obvious questions becomes:
What about infinite continued fractions? Is there a theory of "irrational" tangles?
The irrational tangle corresponding to an infinite continued fraction $$[a_0; a_1, a_2, a_3, \ldots]$$ should of course be the limit (in an appropriate sense) of the sequence of rational tangles corresponding to the sequence $x_k$ of convergents $$ x_k = [a_0; a_1, \ldots, a_k](\infty) \in \Bbb{P}^1(\Bbb{Q})$$ of the real number $x = \lim_{k \rightarrow \infty} x_k$ defined by that continued fraction, so that in the end you get something that looks like a wild knot (see the picture here). In particular, one might hope that there is a $\text{PGL}_2(\Bbb{Z})$-equivariant map $$ \Bbb{P}^1(\Bbb{R}) \longrightarrow \frac{\text{$2$-tangles}}{\text{equivalence}} $$
Has such a theory ever been worked out?