How to add essentially new knots to the universe?

Question

A knot is an embedding of a circle $S^{1}$ in $3$-dimensional Euclidean space, $\mathbb{R}^3$. Knots are considered equivalent under ambient isotopy. There are two different types of knots, tame and wild. A tame knot is any knot equivalent to a polygonal knot, that is a knot whose image in $\mathbb{R}^3$ is the union of a finite set of line segments. A wild knot is a knot that is not tame. In contrary to the tame knots, wild knots are not well-behaved creatures. They often provide counterexamples to the general version of those theorems which hold for the tame knots.

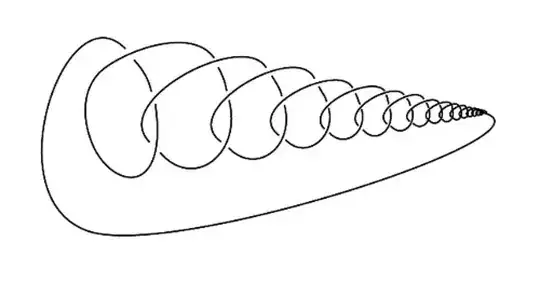
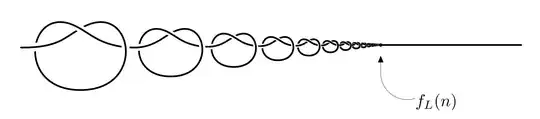
There are several invariants associated with the knots. For example, the crossing number of a knot is a knot invariant defined as the smallest number of crossings of any diagram of the knot. Wild knots (such as the following picture) may have infinite crossing numbers anywhere between $\aleph_0$ and $2^{\aleph_0}$.

Remark 1. Some cautiousness is needed in the previous statement. According to what Joel has mentioned in his comment, the last statement can be made more accurate. In fact, the set of crossing points of a wild knot seems to be projective which implies that assuming the existence of infinitely many Woodin cardinals, it is either countable or of size continuum because the axiom of Projective Continuum Hypothesis holds under this plausible large cardinal assumption. Furthermore, based on Andreas' comment, one may remove the large cardinal assumption in the last argument too.

While there has been an extensive amount of research dedicated to the classification of tame knots (particularly the iconic prime ones), up to ambient isotopy, it turned out that the classification of wild knots is generally much more complicated. (In this direction see Kulikov's paper: A non-classification result for wild knots).

My question simply is how to make the chaos caused by wild knots even worse by adding new ones to the universe through forcing.

Question 1. Assuming failure of Continuum Hypothesis, let $\aleph_0<\kappa\leq 2^{\aleph_0}$ be an uncountable cardinal. Is there a cardinal preserving forcing notion $\mathbb{P}$ of the universe $V$ such that in $V^{\mathbb{P}}$ there exists a wild knot $K$ of crossing number $\kappa$ which is different from all wild knots of crossing number $\kappa$ in the ground model up to ambient isotopy (definable in $V^{\mathbb{P}}$)?

Remark 2. Potentially, one may find some questions, related to the possible number/behavior of wild knots of the certain knot invariant (such as bridge, unknotting, stick numbers, etc.) in a forcing extension, interesting. However, for the sake of this question, I preferred to stick to a very specific one concerning crossing number. Please feel free to share your thoughts about other possibly interesting problems along these lines in the comments below.

---

Update. According to Ian's remark in the comments section, it turned out that the notion of crossing number for wild knots retains some ambiguity, as (in contrary to the case for tame knots) there is no straightforward theorem guaranteeing the existence of a regular projection for wild knots, which is somehow essential for counting the number of crossing points in a wild knot. Roughly speaking, if you have a wild knot, you can't even be sure how much knotted it is! Another indication of why these crazy creatures deserve the name "wild"!

Anyway, the soul of the original question remains valid even without any specification to the case of tame/wild knots of any particular characteristics in terms of knot invariants. The main problem is whether it is possible to add a morphologically new knot to the mathematical universe via forcing. Precisely:

Question 2. Starting from a model $V$ of $ZFC$, is there a (cardinal preserving) forcing notion $\mathbb{P}$ in $V$ such that in $V^{\mathbb{P}}$ there exists a (possibly wild) knot $K$ which is different from all knots of the ground model up to ambient isotopy (definable in $V^{\mathbb{P}}$)?

Answer 1

Yes, forcing can add fundamentally new knots, not equivalent to any ground model knot. Indeed, whenever you extend the set-theoretic universe to add new reals, then you must also have added fundamentally new knots.

Theorem. If $V\subset W$ are two models of set theory with the same ordinals and different reals (for example, any forcing extension with new reals), then there are new knots in $W$ not equivalent in $W$ to any ground model knot from $V$.

(Note that indeed it makes sense to consider the ground model knots $k$ as knots in any extension; simply view them as a Borel set, to be re-interpreted as the corresponding Borel set in the extension, constructed according to the same process; the assertion that a given Borel code represents a knot is a $\Sigma^1_1$ property and therefore absolute. One should not think of a ground model knot merely as a point set, since this exact set will no longer be a knot in a forcing extension with new real numbers.)

To prove the theorem, we use the work of Vadim Kulikov, who has already done the heavy knot-tying for this question. Specifically, in his answer to the question on the Descriptive set-theoretic complexity of knot equivalence, Vadim explains that the relation of knot equivalence is strictly above the isomorphism relation of countable structures in the hierarchy of Borel reducibility. This means that there is a Borel map $\pi$ from the space of countable structures to knots, such that structures $A$ and $B$ are isomorphic if and only if knots $\pi(A)$ and $\pi(B)$ are equivalent (but no such map in the other direction).

One should think of the map $\pi$ as a means to code an arbitrary countable structure into a knot. Using $\pi$, one can code a countable graph, group or partial order $A$ into the knot $\pi(A)$, in a way that respects knot equivalence. In this way, Vadim's result fulfills the suggestion I had made in the comments on the question that what we want to do is code arbitrary binary sequence into knots. Given the countable structure $A$, the knot $\pi(A)$ codes $A$ in that we can recover $A$ up to isomorphism from any knot that is equivalent to $\pi(A)$. The recovery process is sufficiently explicit that it is absolute between a model of set theory and its forcing extensions.

This analysis of the complexity of not equivalence is evidently the main result of his paper:

• Kulikov, Vadim, A non-classification result for wild knots, Trans. Amer. Math. Soc. 369 (2017), 5829-5853, ZBL06722528. (arxiv:1504.02714)

Kulikov states that it follows from his theorem that, "wild knots cannot be completely classified by real numbers considered up to any Borel equivalence relation." So there can be no classification of the wild knots along the same lines as the tame knot classification.

My point here is that it follows from the positive part of the reduction — that isomorphism of countable structures reduces to knot equivalence — that in any extension $W$ with new real numbers, there will also be new knots, not equivalent to any ground model knot.

To see this, suppose that $z$ is a real in an extension $W$, but not in $V$. Let $A_z$ be a countable structure, say, a graph, coding $z$ in some fundamental way, making it definable from the theory of this structure. Let $k=\pi(A_z)$ be the associated knot in $W$. I claim that $k$ is not equivalent to any ground model knot. If $k$ were equivalent to some $k'$ in the ground model $V$, then the assertion $\exists y\ k'\sim\pi(A_y)$ is true about $k'$ in $W$. This is a $\Sigma^1_1$ statement about $k'$, which by Lévy absolutelenss must already be true in the ground model. So there is some ground model real $y$ such that $k'$ is equivalent to $\pi(A_y)$ in $V$. Thus, $\pi(A_y)$ and $\pi(A_z)$ are equivalent in $W$, and so $A_y$ must be isomorphic to $A_z$, contradicting that $z$ is not in $V$ and therefore not definable in $A_y$.

So $k$ is a totally new knot, as desired.

This phenomenon is not possible with tame knots. Since there are only countably many tame knots up to equivalence, there is a list of countably many tame knots, and the assertion that every tame knot is equivalent to one of them is a $\Pi^1_2$ assertion about that list. By absoluteness, this remains true in all forcing extensions. So you cannot add fundamentally new tame knots.

(This answer addresses what I take to be the main part of your questions, whether forcing adds new knots, and not specifically about the crossing number issue.)

Answer 2

Awesome. In fact the way I define the reduction of a turbulent equivalence relation into wild knots is by taking infinite descending intersection of knotted tori. This can be directly converted into a forcing notion where the conditions are finite descending sequences of such tori. This forcing will directly give new knots and is probably equivalent to Cohen forcing (I am not sure). But in this way one can have greater control of what kind of a knot one wants to add, e.g. if one is interested in some particular invariants for example.