6

Form this question, I was surprised to learn that it is common for calculus textbooks in the US to allow $r<0$ when discussing polar coordinates. This answer by Dan Fox summarizes some mathematical and pedagogical drawbacks of this. Let me outline them and add some more:

  • If we restrict to $r\geq 0$, then $(r,\theta)$ have a natural geometric meaning - the distance to the origin and the polar angle, the latter defined up to $2\pi$ by necessity. Allowing $r<0$ makes it much messier and necessarily de-emphasizes the important geometric picture.
  • This aligns well with the view that coordinates are functions on the manifold, or, if you wish, that they are numbers assigned to physical points. Then, equations in polar coordinates, such as $r^2=\sin\theta$, simply describe the set of points which satisfy the equation when fed into it (with some choice of a branch for $\theta$), just as it is the case with equations in Carthesian coordinates.
  • An alternative view, as expressed in comments, is that polar coordinates is a map $P:(r,\theta)\mapsto (r\cos\theta,r\sin\theta)$, and the equation denotes an image of the corresponding set in $(r,\theta)$ plane. Apart from a need to re-define the meaning of an equation, in practice one is never interested in an image of a given set under $P$ - rather, one is given a set $V$ in the physical plane and looks for a description of that set in polar coordinates, i.e., a set $U$ such that $P(U)=V$, e.g., to integrate in polar coordinates. In practice, this is nearly always done with the restriction $r\geq 0$, especially since bijectivity on $U$ is desirable.

So, the question is: what are the benefits of allowing $r<0$? If it is in the textbooks by historical reasons, what was the historical point of view that lead to it? What are some applications of polar coordinates where this is useful?

Kostya_I
  • 1,382
  • 6
  • 12
  • 3
    This is similar to allowing $\theta$ outside $[0,2\pi]$. – Gerald Edgar Mar 08 '24 at 13:14
  • 1
    The answers so far do not seem to adequately address the pedagogical side of this question. Precalc students don't need to care about branch cuts and so on. To me, the benefit of keeping $r>0$ is that it gives students a useful geometric lodestar: $r$ is the distance from the origin. If we throw this away, we should get something very good in return. – user1149748 Mar 08 '24 at 21:24
  • Also: polar coordinates are useful in situations with rotational symmetry, or that are close enough to rotationally symmetric to make polar coordinates a better choice than Euclidean. Conveniently describing a line through the origin, or a circle not centered at the origin, does not strike me as convincing because polar coordinates aren't made for these tasks. – user1149748 Mar 08 '24 at 21:28

5 Answers5

10

There is still a simple geometric meaning for polar coordinates when we allow for negative values of $r$. (It's how I was taught polar coordinates.) Given an ordered pair $(r, \theta)$,

  1. Start at the origin facing the polar axis.
  2. Rotate by the directed angle $\theta$. (Counterclockwise if $\theta>0$ and clockwise if $\theta<0$.)
  3. Travel the directed distance $r$. (Forwards if $r>0$ and backwards if $r<0$.)

This does not fit the notion of a coordinate chart, which should assign to each point a unique list of coordinates. But it makes perfect sense as a coordinate transformation, which assigns to each list of coordinates a point. If we restrict $P$ to the domain $[0, \infty) \times [0, 2\pi)$, then we have an (almost) bijection that can be used to define a coordinate chart. But it is sometimes more convenient to restrict to $\mathbb{R}\times(-\frac{\pi}{2},\frac{\pi}{2}]$. And when we don't need a coordinate chart and bijectivity isn't important, why not allow for the domain to be $\mathbb{R}^2$?

I'm not sure what you mean by needing to "re-define the meaning of an equation." I was taught that an equation is an open statement of equality involving some number of free variables. The solutions of an equation, given an ordering of the variables, are lists of values that satisfy the equation. To produce a graph of an equation, we interpret the solutions as coordinates, then map coordinates to points.

In addition to the examples of circles, spirals, hyperbolas, and roses others have already given, there are many more interesting and beautiful curves generated by simple polar equations that rely on negative values of $r$ and/or values of $\theta$ outside of $[0, 2\pi)$. For example, the graph of $r=\frac{1}{2}+\cos(\theta)$ is a limaçon with an inner loop.

Graph of r=1/2 + cos(theta), a limaçon with an inner loop.

Here's another situation where it makes perfect sense to use negative values of $r$. Consider a particle traveling down the $y$-axis whose position in Cartesian coordinates is described by $\mathbf{r}_\text{C}(t)=(0, 1-t)$. Its position in polar coordinates can be described simply as $\mathbf{r}_\text{P}(t)=(1-t,\frac{\pi}{2})$. This matches our sense that the particle never "changes direction," even while passing through the origin. But if negative values of $r$ are not allowed, the parametrization must be discontinuous at $t=1$: $\mathbf{r}_\text{P}(t)=(1-t,\frac{\pi}{2})$ for $t\leq1$ and $\mathbf{r}_\text{P}(t)=(t-1,\frac{3\pi}{2})$ for $t>1$. The same applies to almost any other smooth path through the origin.

Justin Hancock
  • 3,050
  • 6
  • 23
  • I think you answer sheds some light on the question "how did it get into textbooks": it came from the times when "function" meant an analytic function and "curve" meant an (entire) analytic branch; so restriction to $r>0$ would sometimes mean that we abruptly cut such a branch and "lose a part of it". Since this point of view is entirely abandoned elsewhere in curricula now, I don't see a good reason to stick to it here either. – Kostya_I Mar 08 '24 at 22:27
  • In usual professional mathematical usage "coordinates" mean a bijective map (with some further restrictions depending on the category in which one works). The idea is that coordinates should uniquely specify a point on the space under consideration. There is nothing wrong with allowing negative r, but it seems to me an error to refer to such as a "coordinate". – Dan Fox Mar 20 '24 at 07:07
8

It would be nice if we distinguished between "polar coordinates" and "polar parameterizations".

Let $\Omega \subset \mathbb{R}^2$ be an open set which does not contain any loop around the origin. Then a choice of polar coordinates for $\Omega$ is a choice of smooth section of $P$. Such a section always exists and, if $\Omega$ is connected, the section is completely determined up to a sign of $r$ and a multiple of $2\pi$ for $\theta$. You are correct that we never have polar coordinates where $r$ changes sign.

On the other hand, we can describe some subsets $S_{x,y} \subset \mathbb{R}^2$ conveniently using polar parameterizations. A polar parameterization is just describing $S_{x,y}$ as $S_{x,y} = P(S_{r,\theta})$ for some $S_{r,\theta} \subset \mathbb{R}^2$. Note that polar coordinates are polar parameterizations, but not all polar parameterizations are polar coordinates!

When we write "polar equations" are are actually talking about polar parameterizations, not polar coordinates. Let's look at the equation $r = \cos(\theta)$, with $\theta \in [0,\pi]$ to describe a circle.

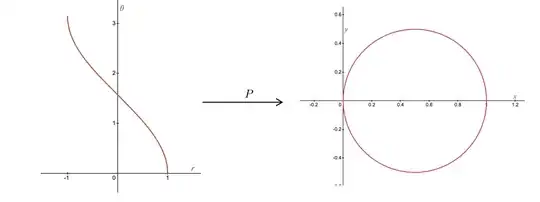
parameterization of circle

Note that the restriction of $P$ from the graph of $r = \cos(\theta)$, with $\theta \in [0,\pi]$, is smooth through $r=0$! This is as nice as it gets.

In general if $f: (\theta_1, \theta_2) \to \mathbb{R}$ is any smooth function, the map $\theta \mapsto (f(\theta),\theta) \mapsto P(f(\theta),\theta)$ will also be smooth. When we write $r = f(\theta)$ for $\theta \in (\theta_1, \theta_2)$ we are actually thinking about a parameterized curve in the $(x,y)$ plane. We are not (as you claim in the OP) graphing the equation $r = f(\theta)$ where $(r,\theta)$ are polar coordinates for some region containing the circle (in fact, no such polar coordinates exist since no region containing the origin has a smooth section).

Usually you will not want to include a point where $r = 0$ even in a parameterization of a 2D region, since $P$ is locally "two to one" on any punctured neighborhood of a point $(0,\theta_0)$.

However, there are even circumstances when this is natural. When I want to find the area of the disk bounded by $r = \cos(\theta)$, it is natural to use an integral from $\theta = 0$ to $\theta = \pi$.

enter image description here

It is still one to one and nice enough that you can write the whole area of the disk as

$$ \int_0^\pi \cos^2(\theta)\textrm{ d}\theta $$

with no issue (breaking it up from $0$ to $\frac{\pi}{2}$ and $\frac{\pi}{2}$ to $\pi$ gives two nice non-overlapping pieces).

I wouldn't usually think about the pre-image when I write down this integral: I just think about cutting the disk into small pieces.

While I agree that for many purposes it is nice to restrict to $r>0$ it is not always needed.

I want to illustrate how a region can have polar coordinates without restricting $\theta \in [0,2\pi)$. For example, $P$ restricts to a diffeomorphism between the rectangle $(0.5,3) \times (0,6\pi)$ in the $(r,\theta)$ plane and the region $ 0.5 + \theta < r < 3 + \theta$ with $\theta \in (0,6\pi)$. I would like to be able to work with this region without breaking it up into chunks which are artificially restricted to only go from $\theta = 0$ to $\theta = 2\pi$.

spiral region

I will also note that contending with these kinds of issues is bread and butter stuff in complex analysis.

EDIT: One more note. The OP says that:

This aligns well with the view that coordinates are functions on the manifold, or, if you wish, that they are numbers assigned to physical points. Then, equations in polar coordinates, such as $r^2 = \sin(\theta)$, simply describe the set of points which satisfy the equation when fed into it (with some choice of a branch for $\theta$ ), just as it is the case with equations in Cartesian coordinates.

This point of view has a few serious drawbacks.

First of all $\theta$ is not a coordinate map. It is locally but not globally. Hence the need for a choice of the branch.

More seriously, this interpretation of a "polar equation" never admits $r=0$ as a solution. Let's be explicit and attempt to define

$$r(x,y) = \sqrt{x^2 + y^2}$$

$$ \theta(x,y) = \operatorname{atan2}(x,y) $$

See this definition of $\operatorname{atan2}(x,y)$.

Then according to OP definition a solution of $r^2 = \sin(\theta)$ is a point $(x,y)$ satisfying

$$ x^2 + y^2 = \sin(\operatorname{atan2}(x,y)) $$

Since $\operatorname{atan2}(0,0)$ we must admit that $(0,0)$ is not a solution of $r^2 = \sin(\theta)$ under the definition of the OP.

This is not to say that this is a poor definition: it is good for some purposes and not for others.

Steven Gubkin
  • 25,127
  • 4
  • 61
  • 110
  • 1
    I agree that not restricting $\theta$ to $[0,2\pi)$ is fundamental. But in the first example, what are the advantages compared to taking $\theta\in[-\pi/2,\pi/2)$ (or, if you wish, $\theta\in[0,\pi/2)\cup[\frac{3\pi}{2},2\pi)$?) – Kostya_I Mar 08 '24 at 15:17
  • 2
    I am saying that, for curves, "$r = f(\theta)$" is a convenient shorthand for $\theta \mapsto (f(\theta)\cos(\theta),f(\theta)\sin(\theta))$: a perfectly respectable parameterized curve no matter the sign of $f(\theta)$. – Steven Gubkin Mar 08 '24 at 15:19
  • If you really want to be consistent and say that "coordinates are functions on the manifold", then you have to deal with the issue of branch cuts. My definition of "a choice of polar coordinates" above is the only rigorous fix I am aware of. Restricting $P$ to $r > 0$ and $\theta \in [0,2\pi)$ is not really "coordinates" by that definition either. It only gives us coordinates for $\Omega = \mathbb{R}^2 - {(x,0): x \geq 0}$. – Steven Gubkin Mar 08 '24 at 15:25
  • If you want a looser definition of coordinates, so that for you $r: \mathbb{R}^2 - {0,0} \to (0,\infty)$ and $\theta: \mathbb{R}^2 \to S^1$ (as you seem to imply when you say that $\theta$ is only defined up to $2\pi$), then your "polar coordinates" do not function at the origin. It would not be legit to ever use $r=0$ or describe the point $(0,0)$ with these coordinates. So the circle centered at $(0.5,0)$ of radius $0.5$ is simply not expressible using your coordinates. – Steven Gubkin Mar 08 '24 at 15:34
  • I don't know why you are dwelling on the origin so much: I'm happy to exclude the origin; polar coordinates are badly behaved there either way. I see no natural reason why the curve $r=\sin\theta$ must contain the origin but the logarithmic spiral $r=e^\theta$ must not. – Kostya_I Mar 08 '24 at 22:10
  • @Kostya_I My point is that your claim that polar coordinates are "coordinates" is flawed in two ways: (1) they do not work at the origin. Sure you can fix that by saying polar coordinates do not work there, and a polar equation will never have the origin as a solution, but I will note that you yourself initially include the origin in the solution set. (2) The issue of $\theta$ only being well defined up to a multiple of $2\pi$ is serious. I am curious why you stick with a polar equation having a "coordinate" interpretation when they are not valid coordinates. – Steven Gubkin Mar 09 '24 at 11:19
  • By comparison, interpreting $r=\sin(\theta)$ as shorthand for $\theta \mapsto (\sin(\theta)\cos(\theta),\sin(\theta)\sin(\theta))$ seems a mild abuse. It also agreed with Justin's geometric interpretation of $r$ as a directed distance from the origin, and $\theta$ as a directed angle from the polar axis. – Steven Gubkin Mar 09 '24 at 15:05
  • My rigorous definition of "a set of polar coordinates" clarifies these issues (1) and (2). You cannot have polar coordinates on the whole plane, or even the whole plane minus the origin. You can only have them on a subset which does not contain a loop around the origin. One standard such domain is $\mathbb{R}^2 - {(x,0): x \leq 0}$, and then it is common to have $\theta \in (-\pi,\pi)$. I do not see why you consider this less of a serious issue for the "solution set of an equation" than the issue of negative $r$. – Steven Gubkin Mar 09 '24 at 15:10
4

Allowing $r<0$ certainly does not de-emphasize the geometric picture. The image below is the graph of $r=\sin(3\theta).$ As $\theta$ goes from $0$ to $\pi/3,$ $3\theta$ goes from $0$ to $1$ and back down to $0,$ $r$ goes from $0$ to $1$ and then back down to $0,$ and you see the part of this figure that is in the first quadrant. It lies below the line $\theta=\pi/3,$ the $60^\circ$ ray. As $\theta$ goes on from $\pi/3$ to $2\pi/3,$ $r$ goes from $0$ to $-1$ and back up to $0,$ giving us the part of this picture that is below the $x$-axis. The third leaf, in the second quadrant, has $\theta$ going from $2\pi/3$ to $\pi.$ Then as $\theta$ goes from $\pi$ to $4\pi/3,$ $r$ is negative again and we traverse the first leaf, in the first quadrant, for the second time. And so on. Negative values of $r$ have a natural geometric meaning, just as positive values do.

enter image description here

Michael Hardy
  • 1,885
  • 11
  • 24
3

Polar curves are a very old subject. This article, published in 1949 in the American Mathematical Monthly, suggests that the subject goes back to Newton. Newton as an Originator of Polar Coordinates.

In this framework, we represent curves in the plane by the scheme $R=f(\theta)$. There is simplicity and elegance that would not be present if we decreed that the polar variable $R$ must be positive.

A simple example is the curve $R=\cos(\theta)$. If there is a rule forbidding $R<0$ then we are stuck with a semicircle. But without the restriction, the graph is the entire circle, traversed for $\theta\in[0,\pi]$.

Another example is the equation of a conic in polar coordinates. A very general form is $$R=\frac{l}{1-e\cos(\theta)}$$ where $e$ is the eccentricity. The equation unifies conic sections. But alas, if we had to live under a regime where $R<0$ is forbidden, the hyperbolas would be missing one of their branches.

It is also amusing to think about what would happen to curves like the four-leaf rose $R=\cos(2\theta)$. I suppose we would have to rename it, since it would have just two lobes. Even then it is awkward because you have to wait and look the other way while $\theta$ progresses through the intervals where $\cos(2\theta)<0$.

user52817
  • 10,688
  • 17
  • 46
  • 1
    Sorry, I don't follow. You don't need $R<0$ for the equation "$R=\cos \theta$" to describe the full circle; just use the range $-\frac{\pi}{2}\leq\theta<\frac{\pi}{2}$, which is also geometrically the range of polar rays that do intersect the circle. In other two examples, taking the absolute value, or squaring both sides, restores all the desired branches. – Kostya_I Mar 08 '24 at 14:58
  • 2
    @Kostya_I The fact that you have to futz around with domain restrictions is unnecessary overhead, resulting from requiring $r>0$. – user52817 Mar 08 '24 at 15:54
  • 1
    if you prefer $[0,2\pi)$ as the domain, the equation $r=\cos\theta$ still describes the full circle. A semi-circle only entered the picture because you futzed around with the domain. – Kostya_I Mar 08 '24 at 16:09
  • @Kostya_I You want the equation $r = \cos(\theta)$ for $\theta \in [-\frac{\pi}{2}, \frac{\pi}{2}]$ to mean "the set of all allowable point $(x,y)$ where the equation $r(x,y) = \cos(\theta(x,y))$ is satisfied, given my definition of the functions $r$ and $\theta$". You must then admit that $(x,y) = (0,0)$ is not in the solution set, as $\theta$ is undefined at $(x,y) = (0,0)$. It only makes sense to include $(0,0)$ in the solution set if $r=\cos(\theta)$ is interpreted as a parametric curve. When you do this, there is no need to restrict $r>0$: it is artificial. – Steven Gubkin Mar 08 '24 at 17:06
1

There is a clear interpretation of negative angles, and we allow angles to be negative. There is a clear interpretation of negative radii, so it's only natural (or at least "consistent") to do the same and allow radii to be negative.

Sure, there are some more advanced contexts where that causes an issue. But we can resolve those issues when we get to them (by introducing the restriction that radii are to be non-negative in those contexts).

Justin Skycak
  • 9,199
  • 4
  • 27
  • 47
  • 3
    Given the very different sorts of roles played by angles and radii in polar coordinates, it makes no sense to say that it's only natural to do the same things with one that one does with another. There are reasons to allow radii to be negative, but that can't be it. – Michael Hardy Mar 08 '24 at 17:23
  • @MichaelHardy okay, then replace the word "natural" with "consistent". – Justin Skycak Mar 08 '24 at 20:17