Intuition for order of operations in compound transformations

Question

This is a close cousin of the previous question asked here about transformations inside and outside a function and how they switch things around. I think some of the perspectives there will help here, but I'd also be interested in something specific to this issue.

Consider a question like

Graph $y=\sqrt{2x-6}$ by starting with the graph of $y=\sqrt{x}$ and applying a series of transformations.

For many of my students, their thought process goes like "$2x-6$ means 'multiply by $2$ then add $6$', so my transformations should go $$\sqrt{x} \rightarrow \sqrt{2x} \rightarrow \sqrt{2x-6}$$

meaning I should start with my graph of $\sqrt{x}$, shrink it horizontally by a factor of $2$, and then to the right by $6$."

While I can explain to them where their second transformation goes wrong, I have a harder time helping them understand how to figure out proper ordering of steps. Whether you write things as $$\sqrt{x} \rightarrow \sqrt{2x} \rightarrow \sqrt{2(x-3)}$$ or $$\sqrt{x} \rightarrow \sqrt{x-6} \rightarrow \sqrt{2x-6},$$ either way goes in the reverse of the usual order of operations.

Is there a good intuitive explanation for how to think about the order of steps when constructing these compound transformations?

Answer 1

For teaching this concept, I always come back to tables of values. In Calculus Reform, there was the "Rule of Three" which emphasized that learning about functions should involve tables, graphs, and algebraic formulas. We should always be able to see a function concept from all three angles. In teaching, we tend to skimp on the "table" perspective.

Scaffold this for your students. Let $f(x)=\sqrt{x}$ with domain $0\le x\le 4$. Draw the square root curve with points $(0,0),\ (1,1),\ (4,2)$ emphasized. Notice the graph ends at $(4,2)$!

Next make a table of values for $y=f(x)$ like this

\begin{array}{c|c} x & f(x)=\sqrt{x} \\ \hline 0 & 0 \\ 1 & 1 \\ 4 & 2 \\ \end{array}

The next step is a table of values for $g(x)=f(2x)=\sqrt{2x}$. A learning moment ensues while we thrash around, trying to figure out the domain for $g$. It is $0\le x\le 2$. We reward ourselves with the template for our next table:

\begin{array}{c|c} x & y=\sqrt{2x} \\ \hline 0 & \\ 0.5 & \\ 2 & \\ \end{array} Filling in the second column feels "just right" because it links so nicely with the first table.

Next, we turn to $h(x)=f(2x-6)$. Another learning moment ensues as we thrash around to figure out the domain for $h$. It is $3\le x\le5$. We get rewarded again with the template for our next table:

\begin{array}{c|c} x & y=\sqrt{2x-6} \\ \hline 3 & \\ 3.5 & \\ 5 & \\ \end{array}

Filling in the second column is again satisfying, because it just clicks. But it does not link very nicely with the previous table.

So now we regroup and take a tricky turn and try to relate the column for $x$ in the second table to the column of $x$ for the third table. Upon reflection, we see the differences of 3. Point out how it might have been slicker to have used something else for our second table, namely a table for $\sqrt{x-3}$ instead:

\begin{array}{c|c} x & y=\sqrt{x-3} \\ \hline 3 & \\ 4 & \\ 7 & \\ \end{array}

then followed with our third table (already existing!) for $\sqrt{2(x-3)}$

The moral of the discovery is that the insightful sequence is $x\to (x-3)\to 2(x-3)$, as opposed to the first sequence that started off as $x\to 2x\to\ .$ So the function concept from the graphical perspective (Rule of Three) is to first shift the graph by 3, then compress.

Answer 2

One way to build intuition around this is to think about the effects on the intercepts.

Vertical Shifts/Stretches: Effect on $y$-Intercept

Suppose you want to graph $y=2\sqrt{x}-6$ using transformations.

You know the result needs to have a $y$-intercept of $-6$ (which comes from evaluating $2\sqrt{0}-6$).

• If you stretch vertically by a factor of $2$ and then shift $6$ down, you get a $y$-intercept of $-6$ as desired. $\color{green}\checkmark$

• If you shift $6$ down and then stretch vertically by a factor of $2,$ you get a $y$-intercept of $-12$ which is incorrect. $\color{red}\times$

So vertical stretches come before vertical shifts.

Horizontal Shifts/Shrinks: Effect on $x$-Intercept

Suppose you want to graph $y=\sqrt{2x-6}$ using transformations.

You know the result needs to have an $x$-intercept of $3$ (which comes from solving $0=\sqrt{2x-6}$).

• If you shrink horizontally by a factor of $2$ and then shift $6$ right, you get an $x$-intercept of $6$ which is incorrect. $\color{red}\times$

• If you shift $6$ right and then shrink horizontally by a factor of $2,$ you get an $x$-intercept of $3$ as desired. $\color{green}\checkmark$

So horizontal shifts come before horizontal shrinks.

---

More Hand-Wavy (But Potentially More Memorable) Intuition

When it comes to horizontal transformations, everything works the opposite way as vertical transformations.

The transformations themselves are opposite:

• shifts right (the negative horizontal direction) instead of shifts up (the positive vertical direction)

• horizontal shrinks instead of vertical stretches

So it's kind of intuitive that the order of transformations is also opposite.

Answer 3

I'd say the root cause of your problem is that you're forgetting to include the square root in the sequence of operations transforming $x$ into $\sqrt{2x-6}$:

$$ x \overset{\times 2}{\ \to\ } 2x \overset{-6}{\ \to\ } 2x-6 \overset{\sqrt\cdot}{\ \to\ } \sqrt{2x-6} $$

Having written out the entire chain of transformations like this, you can then obtain the graph of the compound transformation by starting with the trivial graph of $y = x$ and going backwards along this chain, undoing each operation one at a time:

• Conveniently, we've already been given the graph of $y = \sqrt x$, so that's the last step in the chain already taken care of. (Which is nice, because the inverse of taking the square root is squaring, and that's a non-linear transformation that changes the shape of the graph in more complicated ways than just simple shifting and scaling.)

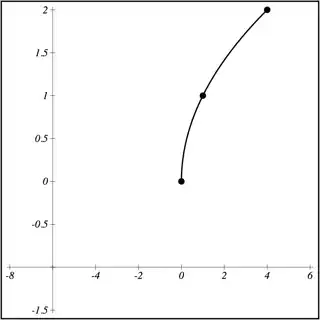
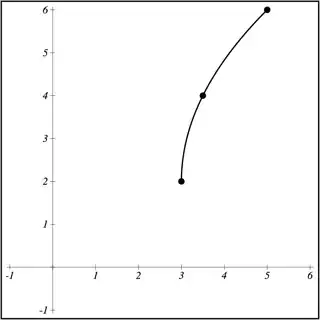
• Now, the previous operation in the chain, just before the square root, is the subtraction of $6$. Thus, to turn the graph of $y = \sqrt x$ into the graph of $y = \sqrt{x-6}$, we need to undo the subtraction by adding $6$ to the $x$-coordinate of each point on the graph, i.e. by moving the entire graph $6$ units to the right.

• The step before that (and the first step in the whole chain) is then the multiplication by $2$. Thus, to turn the graph of $y = \sqrt{x-6}$ into the graph of $y = \sqrt{2x-6}$, we need to undo the multiplication by halving the $x$-position of each point on the graph, i.e. shrinking the graph horizontally by a factor of 2 towards the origin.

---

A pedagogical note that should be emphasized here, in order to turn this method from rote memorization into actual understanding, is that each step in the forwards chain above corresponds to applying a transformation to the result of the previous transformations (i.e. to the entire expression). On the other hand, in the backwards chain:

$$ \sqrt{2x-6} \overset{\times 2}{\ \leftarrow\ } \sqrt{x-6} \overset{-6}{\ \leftarrow\ } \sqrt{x} \overset{\sqrt\cdot}{\ \leftarrow\ } x $$

we're applying each operation to the inputs of the later transformations, i.e. to each $x$ in the expression. And this replacement of each $x$ in the expression with something else (e.g. $\sqrt x$, $x-6$ or $2x$) is graphically equivalent scaling the $x$-axis of the graph.

Another useful way of looking at this is that if we change the expression by replacing $x$ with something else, and still want to get the same values out of it, we need to adjust the values of $x$ we're feeding into the expression in the opposite way.

• So, for example, if we change $\sqrt x$ into $\sqrt{x-6}$ (or any $f(x)$ into $f(x-6)$), we now need to make each $x$ we input into the expression bigger by 6 to compensate, which is equivalent to moving the graph 6 units to the right.

• And similarly, when we change $\sqrt{x-6}$ into $\sqrt{2x-6}$ (or any $f(x)$ into $f(2x)$), we now need to make each $x$ we input into the expression only half as big to compensate, which is equivalent to horizontally shrinking the graph by a factor of 2 towards the origin.

There's also a parallelism here between changes to the input and the output of the expression: transforming the input (i.e. replacing each $x$ in the expression with something else) is equivalent to scaling the $x$ axis of the graphs, whereas transforming the output (i.e. applying an operation to the value of the entire expression as a while) is equivalent to scaling the $y$ axis.

Indeed, as an advanced exercise / demonstration, you could try obtaining the graph of something like $y = 3\sqrt{2x - 6} + 1$ starting from the graph of $y = \sqrt x$, where you now need to apply transformations both to the $x$ axis (in "reverse" order) and to the $y$ axis (in "forward" order).

(Also useful may be giving the students the graph of e.g. $y = \sqrt{x} - x$ and having them transform it into the graph of e.g. $y = \sqrt{2x} - 2x$, just to illustrate the point that the reverse transformations need to be applied to each $x$ — and that this trick straight up doesn't work for something like, say, $y = \sqrt{2x} - 3x$, at least not without using transformations more complex than just simple orthogonal scaling and shifting).

---

Also, if your students are already familiar with function notation, you can and should tie this in with function composition. For example, in your original example, $y = \sqrt{2x - 6}$ can be written as $y = h(g(f(x)))$, where $f(x) = 2x$, $g(x) = x - 6$ and $h(x) = \sqrt x$, or equivalently drawn as:

$$ x \overset{f}{\ \to\ } 2x \overset{g}{\ \to\ } 2x-6 \overset{h}{\ \to\ } \sqrt{2x-6} $$

And then you can point out that going from, say, $f(x) = 2x$ to $g(f(x)) = 2x-6$ means applying $g$ to the result of evaluating $f(x)$, whereas going from $h(x) = \sqrt x$ to $h(g(x)) = \sqrt{x - 6}$ means applying $g$ to the input of $h$ before evaluating it.

Answer 4

I think that my previous answer addresses this. If we name the intermediate functions, and make the relationships between these functions explicit, things become a bit easier to understand.

In your example you have $f(x) = \sqrt{2x - 6}$. We want to start with $g_0(x) = \sqrt{x}$ and find an intermediate function $g_1$ so that the graphs of $g_0$ and $g_1$ are related by a basic transformation and the graphs of $g_1$ and $f$ are related by a basic transformation.

If you try what your students suggest then our intermediate function is $g_1(x) = \sqrt{2x}$. We have $g_1(x) = g_0(2x)$, so the graph of $g_1$ is "shrunk horizontally" by a factor of $2$ relative to $g_0$.

Now we want to try to relate $g_1$ to $f$.

$g_1(x) = \sqrt{2x}$ and $f(x) = \sqrt{2x - 6}$. Your student now wants to use a horizontal translation. It might be helpful to get this up as a fill in the blank.

$$ \begin{align*} f(x) &= g_1(x - \square )\\ \sqrt{2x-6} &= \sqrt{2(x - \square)}\\ \sqrt{2x-6} &= \sqrt{2x - 2\square)}\\ \end{align*} $$

It is now clear that we should be taking $\square = 3$ not $\square = 6$.

Answer 5

You can perform the transformations in any order you want as long as you respect this rule:

• Always transform completely inside, affecting $x$ directly, or completely outside, affecting $y$ directly.

If you're only teaching about horizontal stretches and shifts and don't care about vertical stretches and shifts yet, then you can discard the second part, and keep only this one rule:

• Always transform completely inside, affecting $x$ directly.

As long as the students respect this rule, you don't have to teach them a procedure to deduce a possibly-counterintuitive correct order of operations. Just let them work on examples and make sure they respect this one rule.

For instance, to go from $y = \sqrt x$ to $y = \sqrt{2x - 6}$, if a student tries to replace $x$ with $2x$ first, then they cannot replace $2x$ with $2x-6$ next, because that's not a known transformation. The only thing they're allowed to do is replace $x$ with $x-...$ or with $...\times x$. Replacing $2x$ with $2x-6$ is not part of the transformations we have learned.

So the student can either do: $$y=f(x) \quad\to\quad y=f(2x) \quad\to\quad y=f(2(x-3))$$ or: $$y=f(x) \quad\to\quad y=f(x-6) \quad\to\quad y=f(2x-6)$$ but this doesn't work: $$y=f(x) \quad\to\quad y=f(2x) \quad\not\to\quad y=f(2x-6)$$ This is not because of a rule about order of operations, it's because of the one rule about only ever transforming $x$ directly and never transforming $2x$. If you try to do the $2\times...$ first, then you cannot do the $...-6$ because the $...-6$ is not applied to $x$, it's applied to $2x$.

Note that if the expression of $f(x)$ contains more than one occurrence of symbol $x$, you must apply the transformation to every occurrence of $x$. For instance, to shift the graph of $y=x(2x+1)$ horizontally by 5 right you can do: $$y=x(2x+1) \quad\to\quad y=(x-5)(2(x-5)+1)$$ or: $$y=2x^2 + x \quad\to\quad y = 2(x-5)^2 + (x-5)$$

Answer 6

Is there a good intuitive explanation for how to think about the order of steps when constructing these compound transformations?

Here's a stab at what it would mean to obey the order of operations. Note: In what follows, I am using the interpretation of curve transformations to mean we are transforming the underlying axis, not moving a curve around on the plane. I don't think I would ever teach this interpretation like this, but here is how one might just follow the order of operations to correctly draw a transformed function.

Example:^* Suppose we want to graph the curve $\frac{1}{2}y - 1 = \sqrt{2x-6}$.

Let's first graph the standard function $y=\sqrt{x}$.

Now start changing the horizontal axis. We multiply the values on the $x$-axis by a factor of 2 (making it the $2x$-axis). Redraw the curve:

Next, subtract 6 from the values on the $2x$-axis (making it the ($2x-6$)-axis). Redraw the curve:

Now start changing the vertical axis. We multiply the values on the $y$-axis by $\frac{1}{2}$ (making it the $\frac{1}{2}y$-axis). Redraw the curve:

Next, subtract 1 from the values on the $\frac{1}{2}y$-axis, (making it the ($\frac{1}{2}y-1$)-axis):

Finally, put this curve back on the original $xy$-plane:

This is the correct curve which we found by altering the two coordinate axes by just using the order of operations. Note: This is entirely different from how I have ever taught function transformations -- I just wanted to think through how one might obey the order of operations and get the right curve.

Incidentally, it made me think of a simpler task: Solving a linear equation. Try this same thing out with one axis in order to solve for $x$.

Example: Solve the equation $4x-5=-3$.

First, just plot the number $-3$ on the $x$-axis:

Next, multiply the values on the $x$-axis by 4 (making it...you guessed it, the ($4x$)-axis). Redraw the point:

This updates the equation, which now says that $4x=-3$ if $x=-\frac{3}{4}$.

Then subtract 5 to the values on the ($4x$)-axis (making it the ($4x-5$)-axis). Redraw the point:

This again updates the equation, which says that $4x-5=-3$ if $x = \frac{1}{2}$.

Summary: There's probably nothing novel about this, but I just wanted to see what it would mean to strictly follow the order of operations in a transformation, since that's what your students feel we should be doing. My takeaway here is that while it does work, it is perhaps more work than we want to take on in class.

_{[^*I am purposefully not isolating $y$ here in order to avoid the inconsistencies we have to explain to students -- the first being that when we solve for $y$, then any outside change to a function behaves opposite to an inside change. I.e. $y=(x-5)^2 + 3$ involves positive movements in both $x$ and $y$, though one is brought about by subtraction, and the other by addition.]}