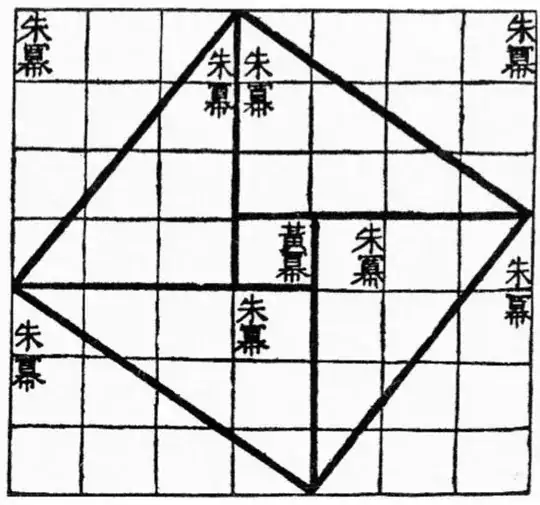
A well-known proof of the Pythagorean Theorem is illustrated in the figure below:
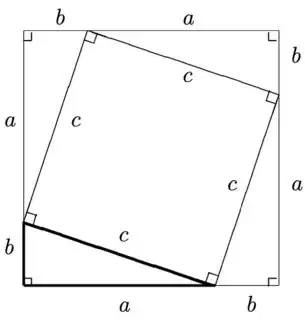
This figure shows a square with side lengths $a + b$, dissected into four right triangles (each with area $\frac 12 ab$) and a square (of side $c$). A basic area computation shows that $(a + b)^2 = 2ab + c^2$, from which one can conclude that $a^2 + b^2 = c^2$.
It's notable that the proof corresponding to this diagram is not the same as the one found in Euclid's Elements (Book I, Prop. 47). Hence my question: What is the first known appearance of this figure in print? According to the Wikipedia article on the Pythagorean theorem,
English mathematician Sir Thomas Heath gives this proof in his commentary on Proposition I.47 in Euclid's Elements, and mentions the proposals of German mathematicians Carl Anton Bretschneider and Hermann Hankel that Pythagoras may have known this proof.
This would seem to suggest that Bretschneider (d. 1878) and Hankel (d. 1873) published, or at least described, this diagram somewhere in their writings. However, this claim falls short of saying that this proof (or the diagram) originates with them. How far back can this diagram and its corresponding proof be traced?